33. Төртбұрыштылар және олардың негізгі теңдеулері

Төртұштықтар деп электр энергиясының көзіне және қабылдағышқа қосатын екі қысқышы бар (полюстері), электрлік тізбек немесе оның бөлігін айтамыз. Төртұштықтарға трансформаторлар, күшейткіштер, электрлік сүзгі-лер, электр энергиясын тасымалдайтын желілер және т.б. жатады. Сөйтіп, төртұштықтар теориясы бізге бір тәсілмен құрылымдары және жұмыс істеу принциптері әртүрлі жүйелерді талдауға көмектеседі.

Төртұштықтардың шартты түрде бейнеленуі 14.1.суретте көрсетілген

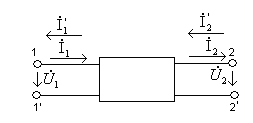
14.1 Сурет

Қысқыштардың екі буыны 1–1’алғашқылар, қос қысқыштар біріншілік деп аталады, екіншілік деп айтылады, электр энергияның көзі қосылған шықпалар кіріс деп аталады, жүктеме қосылған шықпалар шығыс деп аталады. Тоқтар мен кернеулердің оң бағыттары 14.1.суретте көрсетілген.

Активті және пассивті төртұштықтар.

Активті төртұштықтар тәуелді және тәуелсіз энергия көздері бар, пас-сивті төртұштықтарда жоқ.

Сызықты және сызықсыз төртұштықтар.

Сызықты төртұштықтарда сызықсыз элементтер жоқ, ал сызықсыз төртұштықтарда бар.

Қайтымды және қайтымсыз төртұштықтар.

Қайтымды төртұштықтар үшін қайтымдылық және өзаралық теорема-лары орындалады: кернеудің тоққа кірудегі қатынасы шығуда қысқыштардың орын ауыстырғанда өзгермейді. Пассивті төртұштықтар әрқашан қайтымды.

Симметриялы және симметриясыз төртұштықтар.

Симметриялы төртұштықта кіріс және шығыс қысқыштардың орын ауыстыруы тізбектегі тоқтар мен кернеулерді өзгертпейді.

34.Периодикалық синусойдалды емес қисықтарды тригонометриялық қатарларға жіктеу ЭҚК, кернеу, тоқ азды – көпті болса да синусоидальды емес болады. Ол нақты генераторлар қамтамасыз етпейтінімен байланысты, нақты айтқанда, қисық кернеудің синусоидальды түрі және тізбекте сызықсыз элементтің болуы тоқтың бұрмалауына синусоидальды ЭҚК көзі болса да жаңа шарт туғызады. Айнымалы периодикалық синусоидалды емес тоқтың орташа әсерлік мәні

Периодикалық тоқтың әсерлік мәні

.

Периодты синусоидальды емес тоқты тригонометриялық қатарға сала-мыз түрлендіру-ден кейін мынаны аламыз

.

Ұқсас кейіптемелер ЭҚК кернеулерінде де бар

, .

Периодты синусоидальды емес тоқтың тізбектеріндегі қуаты

Кернеу мен тоқтың лездік мәндерін тригонометриялық қатар түрінде жазайық

.

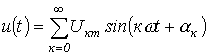
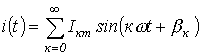Онда, актив қуат үшін былай жазуға болады

Интегралдағаннан кейін аламыз

Осыдан, синусоидальды емес тоқтың актив қуаты актив қуаттардың бөлек гармоникалықтыларына тең болады

.

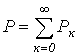Осыған ұқсас реактив қуат үшін жазуға болады:

.

Толық қуат .

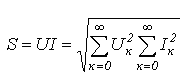Синусоидалы емес ток үшін

Тізбектердегі синусоидальды емес периодты ЭҚК, кернеулерді, тоқтарды есептеу Синусоидальды тоқтың сызықты электр тізбектерін есептеу үш этапқа бөлінеді:

а) синусодалы емес ЭҚК және тоқ көздерін тұрақты және синусоидаль-ды құрастырушыларға ыдырату (Фурьенің тригонометриялық қатарына);

б) ыдырату принципін қолдану және тізбектегі токтар мен кернеулерді әр құраушыға бөлек есептеу. Тұрақты құраушылары бар ЭҚК және тоқ көздері тізбектерін есептегенде мынаны ескеру керек индуктивті кедергі 0 –ге тең және эквивалентті сұлбадағы индуктивтілік қысқаша тұйықталған аймақпен ауыстырылады, ал сыйымдылық тең болады және сыйымдылығы бар бұтақ айырылады. Әр синусоидалы құрастырушы ЭҚК және тоқ көзін есептегенде кешенді әдісті қолдануға болады, бірақ кешенді тоқтарды және әртүрлі синусоидалы құрастырушылардың кернеулерін қосуға болмайды. Міндетті түрде ескеру қажет индутивтілік және сыйымдылық кедергілер әртүрлі жиіліктер үшін бірдей, k-ші гармоника үшін индуктивті кедергі тең болады: , ал сыйымдылық кедергі k-ші гармоника үшін тең болады: ;

в) шешімдерін бірге қарауын, әр құраушы үшін алынған есептерді қарастыру және де құраушы тоқтар мен кернеулердің лездік мәндері ғана қосылады.

35. R,L,C тізбектерін параллель қосу. Егер параллель қосылған r, L, C элементтерінен тұратын u = U_msinωt синусоидалды кернеу тіркелген болса, онда осы тізбекпен өткен синусоидалды тоқ мынаған тең болады

i=i_r+i_L+i_C

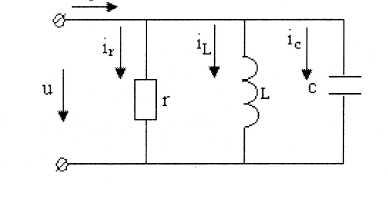
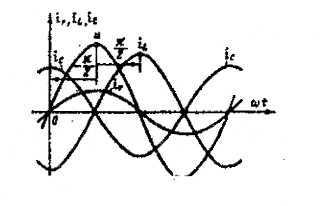
r кедергідегі i_r тоғы фаза бойынша U кернеуімен сәйкес келеді, L индуктивтегі i_L тоғы қалса, С сыйымдылықтағы i_С тоғы π/2 бұрышқа озады.

Сондықтан тізбектегі жалпы тоқ мынаған тең

b=b_L-b_c=(1/ωC)-ωC тізбектің реактивті өткізгіштігі деп аталады да, таң-баға байланысты (b>0) индуктивті сипаттама немесе сыйымдылық сипаттама (b<0) болады. g=1/r – активті өткізгіш деп аталады.

Кирхгофтың бірінші заңы бойынша

İ=gŮ+ Ů+jωCŮ=İ_r+İ_L+İ_C

мұндағы I_r=gŮ – кедергідегі тоқ (фаза бойынша U кернеумен сәйкес келеді).

İ=- Ů - индуктивтіліктегі тоқ

İ=jωCŮ - сыйымдылықтағы тоқ

Кешенді өткізгіш мынаған тең

Y=g-j( -ωC)=g-jb.

Кешенді түрдегі Ом заңының теңдеуі

İ= Y Ů Тригонометриялық және көрсеткіш түрдегі кешендік өткізгіш келесідей болады

Y = у cos φ-jsin φ; Y=ye^{-j φ}

мұндағы у – кешенді санының модулі

Y - тізбектің толық өткізгіштігі

φ – Y кешенді санының аргументі

y=

Кешенді тоқ мынаған тең

i = yUe^J(-)

Бұл синусоидалды тоққа

i = I_m(İ_me^jω) =yU_msin(ωt + ψ - φ)

сәйкес келеді

6.8,a - сурет тізбектің реактивті өткізгіштігі индуктивтілік сипатта (b>0) болғандағы жағдайға ие болып, сонымен қатар тоқ фаза бойынша кернеуден қалады (φ>0). 6.8, б - сурет тізбектің реактивті өткізгіштігі сыйымдылық сипатқа (b<0) ие болып, тоқ фаза бойынша кернеуден озады (φ < 0).

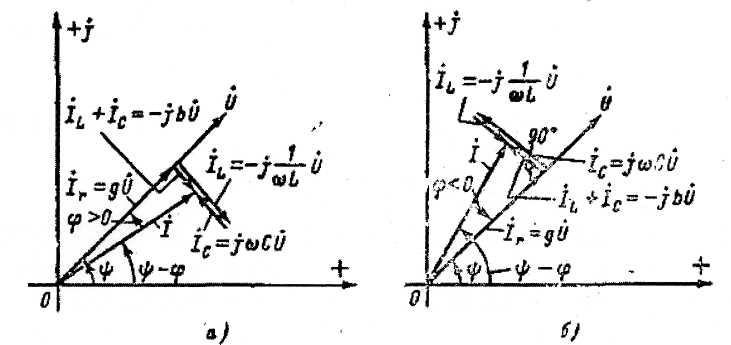
6.8 Сурет