Событие

состоит в том, что все события произошли одновременно.

9. Полная группа событий. Совокупность событий называется полной группой событий, если:

1. Они попарно несовместны, т.е. ,

2. Их сумма (объединение) – достоверное событие, т.е. .

Замечание 1. Если два события A и B составляют полную группу событий, то , т.е. A и B – противоположные события. Действительно, не пересекаются, а .

Замечание 2. Множество всех исходов одного испытания образуют полную группу. Действительно, результатом испытания является один и только один исход. Исходы не пересекаются, а в результате испытания обязательно произойдёт один из них.

Полная группа событий изображена на рис.2.4.12. Круг на первом рисунке и большой прямоугольник на втором рисунке означают пространство элементарных событий (достоверное событие). Секторы круга на первом рисунке и клетки прямоугольника на втором означают события, образующие полную группу.

Пример 16. Появление мастей П, Ч, Т, Б – полная группа событий. Красные и чёрные масти карт тоже образуют полную группу. Кроме того, карты одинакового достоинства: шестёрки, семёрки,..., тузы.

2.5. Свойства операций над событиями

Для произвольных событий непосредственно из определения следует, что

1. А=А 4.

2. 5.

3. 6.

Поясним свойство 6. По определению разности событий это множество элементарных событий, которые входят в А и не входят в В, т.е. тех исходов, которые входят в А и в (рис.2.4.8). Докажите это с помощью диаграммы Венна. Покажем применение этого свойства на примере.

Пример 1. А – выпадение нечётного числа очков при бросании кубика. В – выпадение 1 очка. А–В – выпадение 3 или 5 очков. С другой стороны: – выпадение числа очков, больших 1. Тогда – число очков нечётно и больше 1, т.е. 3 или 5.

Упражнение. Докажите с помощью множества элементарных событий или диаграммы Венна следующие тождества:

7. 10.

8. 11.

9. 12.

Покажем, например, правильность дистрибутивного закона (12) на диаграмме Венна (рис.2.5.1, а, б). На левом рисунке горизонтальной штриховкой отмечена область, соответствующая событию АС, вертикальной штриховкой – событию ВС, косая штриховка на правом рисунке соответствует событию (А+В)С.

а) б)

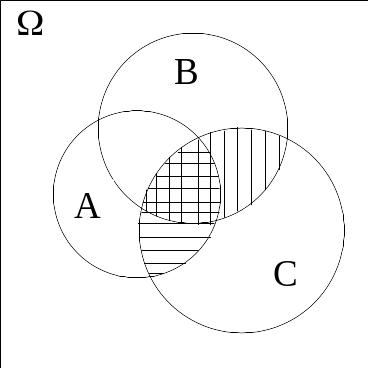
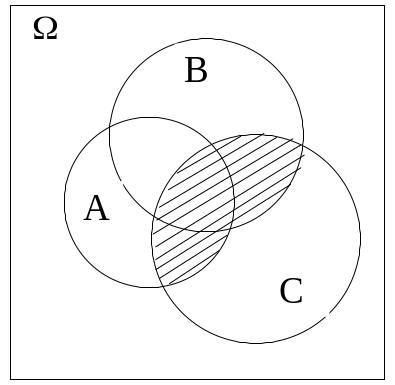
Рис.2.5.1

Приведённые ниже свойства предлагаем читателю изобразить на диаграммах Венна самостоятельно.

13.

14.

15^*.

16^*.

17^*.

18^*. .

Тема: Относительная частота событий и вероятность

3.1 Относительная частота событий

Пусть проводится серия из n испытаний. Рассмотрим некоторое событие А, которое может произойти или не произойти в результате одного испытания. Абсолютной частотой события А в n испытаниях называется число испытаний, в которых событие А произошло. Обозначается k(A). Относительной частотой (А) события А в n испытаниях называется отношение абсолютной частоты к числу испытаний:

(3.1)

Пример. Из 100 деталей, среди которых 3 бракованные, одну за другой вытаскивают и проверяют все детали. Найти абсолютную и относительную частоту события А  «появление бракованной детали».

Решение. k(A)=3; (А)=0,03=3%.

Замечание. В другой партии таких же деталей может быть 2, 4 или 10 бракованных деталей.