11.6. Отклонение случайной величины

от своего математического ожидания

Определение. Разность между случайной величиной и её математическим ожиданием называется отклонением случайной величины Х от своего математического ожидания, или центрированной случайной величиной.

.

Название «центрированная случайная величина» связано с тем, что математическое ожидание есть центр распределения. является смещённой по отношению к Х случайной величиной типа Х+С.

Теорема об отклонении.

Математическое ожидание отклонения равно нулю:

.

Пример. Проводится n измерений некоторого объекта (например, в топографии принято каждый объект измерять не менее 6 раз). Средним значением (математическим ожиданием) будет число, близкое к истинному размеру объекта. Действительно, если при измерении не допускаются систематические ошибки, связанные с особенностями наблюдателя и измерительного прибора, то ошибки положительного и отрицательного знака (отклонения) в среднем будут уравновешивать друг друга. При дальнейшем увеличении числа опытов среднее арифметическое реагирует на это увеличение все меньше и меньше и при достаточно большом числе опытов практически перестаёт меняться:

, или .

Тема: Дисперсия

12.1. Дисперсия Для общего представления о распределении случайной величины важное значение имеет не только её математическое ожидание, но и разброс её возможных значений.

Рассмотрим две случайные величины, имеющие одинаковое математическое ожидание (равное нулю):

X	-0,1	0,1		Y	-100	100
p	0,5	0,5		g	0,5	0,5

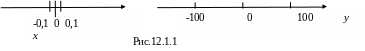Очевидно, однако, что возможные значения случайной величины группируются вокруг математического ожидания неодинаково: значения Х близки к математическому ожиданию, а значения Y расположены от него очень далеко (рис.12.1.1). Другими словами, отклонение Y от своего математического ожидания значительно больше.

В теории вероятностей для измерения разброса значений случайной величины около среднего значения используют понятие дисперсии (dispersio – рассеяние).

12.2. Определение дисперсии

Определение. Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной величины, или квадрата отклонения случайной величины от её математического ожидания:

. (12.2.1)

Таким образом, дисперсия  это средний квадрат отклонения. Отклонения возводятся в квадрат, чтобы их сумма не была равна нулю, что имеет место согласно теореме об отклонении.

Если случайная величина Х дискретна и имеет закон распределения (x_i, p_i) (i=1,2,…, n), то, обозначив МХ=а, из (12.2.1) будем иметь:

Х-MX	х1–a	х2–a	………	хn–a
p	p1	p2	………	pn

(Х-MX)2	(х1–a)2	(х2–a)2	………	(хп–a)2
p	p1	p2	………	pn

. (12.2.2)

В правой части (12.2.2) все слагаемые неотрицательны, следовательно, чем меньше каждое из них, т.е., чем ближе значения случайной величины к математическому ожиданию, тем меньше дисперсия. Это и означает, что дисперсия является характеристикой рассеяния значений случайной величины.

Х	1	2
р	0,3	0,7

Пример. Случайная величина распределена по закону, указанному в таблице. Найти ее дисперсию.

Сначала найдем математическое ожидание:

МХ=10,3+20,7=0,3+1,4=1,7.

Составим ряды распределения для центрированной случайной величины и для её квадрата. Согласно теоремам 2 и 3 о случайных величинах, вероятности при этом не изменятся:

Х–МХ	–0,7	0,3		(Х–МХ)2	0,49	0,09
р	0,3	0,7		р	0,3	0,7

Дисперсия по определению равна математическому ожиданию квадрата центрированной случайной величины:

Если в формуле (12.2.2) заменить на х, на , а сумму на интеграл, то получим выражение для дисперсии непрерывной случайной величины.

Определение. Дисперсией непрерывной случайной величины Х называется число

(12.2.3)

Это определение имеет смысл лишь для таких случайных величин Х, для которых интеграл (12.2.3) сходится.

Если все возможные значения непрерывной случайной величины Х сосредоточены на отрезке [a, b], то:

. (12.2.4)