1.4. Размещения с повторениями (с возвратом)

Пусть имеется некоторая совокупность п различных предметов. Из этой совокупности последовательно выбирается предметов таким образом, что каждый выбранный предмет фиксируется и возвращается обратно. Тогда 1-й предмет выбирается n способами, 2-й – тоже п способами,…, -й – тоже п способами. По правилу произведения число различных комбинаций

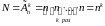. (1.2.3)

Заметим, что в этом случае k может быть > п. Например, разместим 3 предмета в 2 ячейках. . Объект А кладём в 1-ю ячейку, записываем её номер, вынимаем объект. Обе ячейки снова пусты. Получаем (ААА, ААВ, АВА, АВВ, ВАА, ВАВ, ВВА, ВВВ).

Пример 4. В ящике имеется 9 пронумерованных от 1 до 9 шаров. Последовательно вынимается 3 шара следующим образом: номер каждого записывается, после чего шар возвращается обратно. Ясно, что в полученных трехзначных числах цифры могут повторяться. Сколько трехзначных чисел при этом можно получить?

.

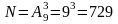Как и следовало ожидать, результат получился больше, чем в примере 1 для размещений без повторений.

Другая формулировка этой задачи: сколько трёхзначных чисел можно получить из 9 цифр от 1 до 9, если цифры могут повторяться?

Пример 5. Замок состоит из 5 дисков с 6 секторами, на которых написаны цифры от 1 до 6 (рис.1.2.1). Диски вращаются вокруг общей оси. Сколько комбинаций нужно перебрать, чтобы открыть замок, если неизвестна установка дисков?

Ясно, что 1-й диск можно установить шестью способами,

2-й – тоже шестью, и т.д. Следовательно,

.

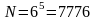1.5. Сочетания

Сочетаниями из п элементов по элементов называются комбинации из элементов, которые отличаются друг от друга только составом элементов.

Из определения сочетания ясно, что порядок расположения элементов внутри комбинации не имеет значения, в отличие от размещения. В данном случае мы рассматриваем неупорядоченные множества из к элементов, выбранных из п-элементного множества. Сочетания обозначаются (це из эн по ка).

Формула для числа всех сочетаний из 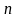по элементов:

. (1.3.1)

Доказательство. Докажем формулу:

(1.3.2)

Действительно, число всех размещений можно пересчитать следующим образом: сначала составим всевозможные сочетания; они будут отличаться только составом элементов; а затем внутри каждого сочетания проделаем всевозможные перестановки. Число этих способов по правилу произведения будет равно левой части формулы (1.3.2). Выразив из (1.3.2) сочетание , с учетом (1.2.2) получим искомую формулу (1.3.1).

Пример 1. Сколькими способами можно составить волейбольную команду из 8 игроков?

.

Пример 2. Сколькими способами в карточке спортлото 5 из 36 можно зачеркнуть 5 номеров (т.е. сколько нужно карточек)?

Число всех способов равно числу сочетаний (порядок зачеркивания не важен):

.

Таким образом, чтобы наверняка зачеркнуть нужную комбинацию из пяти номеров, нужно купить более 370 тысяч карточек.

1.6. Сочетания с повторениями (с возвратом)

Сочетание с повторениями из п элементов по элементов – результат последовательного выбора объектов из совокупности, состоящей из п объектов, при котором выбираемый предмет каждый раз после фиксирования возвращается обратно, а порядок появления объектов несущественен. Если в исходном п-элементном множестве имеются одинаковые элементы, то мы также имеем сочетания с повторениями.

Число сочетаний с повторением из п элементов по дается формулой:

(без доказательства).

Пример 1. Бросают 4 игральные кости и записывают результат. Здесь не принимается во внимание порядок, в котором выпадают цифры. Например, если выпали по порядку 6,6,4,1, а в другой раз – 6,1,6,4, то считают, что эти результаты одинаковы. Фактически здесь имеются сочетания с повторением из 6 элементов (цифр) по 4. Их общее число, т.е. общее число всех возможных результатов, равно

= .

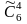Заметим, что число сочетаний без повторений с такими же индексами значительно меньше: 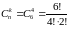=15. Это число выпадений только с различными цифрами.

Пример 2. Количество костей домино в наборе можно рассматривать как число сочетаний из семи цифр (от 0 до 6) по две с повторениями: