7.2. Локальная теорема Муавра – Лапласа

При больших значениях n пользоваться формулой Бернулли трудно, т.к. требуется выполнять действия над очень большими числами. Например, требуется вычислить вероятность ровно 30 выигрышей при покупке 50 лотерейных билетов, если из 1000 билетов 100 счастливых. Здесь n=50, m=30, p=0,1, q=0,9:

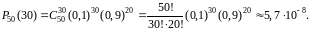
При достаточно больших n удобнее вычислять такие вероятности с помощью асимптотических формул.

Этот вопрос решён с помощью локальной теоремы Муавра – Лапласа. Муавр решил эту задачу в 1730 г. для р=1/2, Лаплас – в 1783 г. для общего случая.

Локальная теорема Муавра–Лапласа. Пусть проводится серия из n испытаний по схеме Бернулли. Если вероятность появления события А в каждом испытании р отлична от 0 и 1, то вероятность Р_n(k) того, что событие А появится в n испытаниях ровно k раз, приближённо равна значению функции

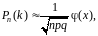(7.2.2)

где q=1–p;

(7.2.3)

(7.2.4)

Функция (х) называется дифференциальной функцией Лапласа.

7.3. Свойства функции (х).

1. . Это видно из формулы (7.2.3). Экспонента всегда положительна.

2. Функция (х) – чётная: (-х)=(х). Это легко проверить, подставив в формулу (7.2.3) (-х) вместо х. График (х) симметричен относительно оси ординат (см. рис.7.2.1).

3. (х)0, когда 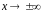, т.е. Это означает, что для одной и той же серии испытаний большие по абсолютной величине х менее вероятны, чем меньшие.

4. При

Для , т.е. порядка одной миллионной.

После вычисления х по формуле (7.2.3) значения функции (х) находят по таблице в приложении к учебникам, другим книгам по теории вероятностей, в справочниках. Таблица дана для положительных х, для отрицательных х пользуются свойством чётности функции (х).

Замечание. Асимптотические формулы применяют, если npq 10.

Пример 1. Вероятность поражения цели стрелком при одиночном выстреле р=0,2. Какова вероятность того, что при 100 выстрелах цель будет поражена ровно 20 раз?

Здесь р=0,2; q=0,8; n=100; k=20. npq=1000,20,8=16>10,

Не следует удивляться, что значение вероятности мало: попадание точно 20 раз при 100 выстрелах есть событие сравнительно редкое! Почти достоверным событием является попадание около 20 раз. Например, вероятность р неравенства , включающего 11 значений k =15, 16,…,24, 25 близка к единице, т.к. каждая из этих вероятностей немногим меньше 0,1. Это можно проверить, вычисляя эту вероятность по формуле

Пример 2. При производстве шестерёнок вероятность брака при штамповке равна 0,1. Какова вероятность того, что из 400 наугад взятых шестеренок 50 будут бракованными?

Здесь n=400, k =50, p=0,1, q=0,9. По формуле Бернулли:

P₄₀₀(50)=

Подсчёт по этой формуле неудобен. Т.к. npq=4000,10,9=36>10, то здесь целесообразно использовать локальную теорему Муавра–Лапласа.

Пример 3. Вероятность поражения мишени стрелком при одном выстреле р=0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

n=10, k=8; p=0,75; q=0,25.

По формуле Бернулли Р₁₀(8)=0,282. Большое расхождение объясняется тем, что формула Муавра-Лапласа дает хорошее приближение только при достаточно больших n и малых р. А в данной задаче npq=100,750,25=1,875<10.