12. Уравнение Эйлера равновесия жидкости.

Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют не только сила тяжести, но и другие массовые силы (сила инерции переносного движения). В неподвижной жидкости возьмем произвольную точку M с координатами x, y и z и давлением p. Система координат жестко связана с сосудом, содержащим жидкость.

Выделим в жидкости элементарный объем в виде прямоугольного параллелепипеда с ребрами, параллельными осям координат и равными dx, dy, dz. Точка M – одна из вершин параллелепипеда (Рис. 3). Рассмотрим условия равновесия этого объема. Пусть внутри его на жидкость действует равнодействующая единичная массовая сила, составляющие которой X, Y, Z. Тогда массовые силы, действующие на выделенный объем в направлении осей, будут равны этим составляющим, умноженным на массу объема жидкости.

Разделим уравнения на массу выделенного объема и перейдем к пределу, устремив dx, dy и dz к 0. Тогда в пределе получим условия равновесия жидкости в точке M (уравнения Эйлера):

На практике вместо системы уравнений удобнее одно эквивалентное уравнение, не содержащее частных производных. Домножим уравнения Эйлера соответственно на dx, dy и dz и сложим их.

Последнее уравнение выражает изменение давления при изменении координат точки.

Рассмотрим частный случай. Пусть из массовых сил действует только сила тяжести. Тогда X = Y = 0, а Z = – g. Тогда полученное уравнение примет вид:

Проинтегрируем уравнение

Константу интегрирования найдем из граничного условия на свободной поверхности:

Тогда

Мы получили основное уравнение гидростатики.

12. Уравнение состояния вещества. Уравнение Клапейрона. Уравнение Клапейрона-Менделеева.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

 — давление,

 — молярный объём,

 — абсолютная температура,

 — универсальная газовая постоянная.

Плотность идеальных газов при давлениях отличных от атмосферного можно опре­делить по известному закону газового состояния Менделеева-Клайперона:

12. Барометрическая формула. Основной закон гидростатики для несжимаемой жид­кости: его энергетическая и геометрическая интерпретация.

Основное уравнение гидростатики

Рассмотрим случай равновесия жидкости в состоя­нии «абсолютного покоя», т.е. когда на жидкость дейст­вует только сила тяжести. Поскольку объём жидкости в сосуде мал по сравнению с объёмом Земли, то уровень свободной поверхности жидкости в сосуде можно счи­тать горизонтальной плоскостью. Давление на свобод­ную поверхность жидкости равно атмосферному давле­ нию р₀. Определим давление р в произвольно выбран­ной точке М, расположенной на глубине h. Выделим

около точки М горизонтальную площадку площадью dS . Построим на данной площадке вертикальное тело, ограниченное снизу самой площадкой, а сверху (в плоскости свобод­ной поверхности жидкости) её проекцией. Рассмотрим равновесие полученного жидкого тела. Давление на основание выделенного объёма будет внешним по отношению к жид­кому телу и будет направлено вертикально вверх. Запишем уравнение равновесия в про­екции на вертикальную ось тела.

Сократив все члены уравнения на dS, получим:

Давление во всех точках свободной поверхности одинаково и равно р₀, следова­тельно, давление во всех точках жидкости на глубине h также одинаково согласно основ­ному уравнения гидростатики. Поверхность, давление на которой одинаково, называется поверхностью уровня. В данном случае поверхности уровня являются горизонтальными плоскостями.

Выберем некоторую горизонтальную плоскость сравнения, проходящую на расстоя­нии z₀ от свободной поверхности, тогда можно записать уравнение гидростатики в виде:

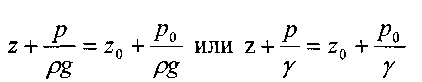
Все члены уравнения имеют линейную размерность и носят название:

z- геометричкская высота,

p/y- пьезометрическая высота

Величина носит название гидростатического напора.

Основное уравнение гидростатики, доказанное на примере жидкости находящейся под действием только сил тяжести, будет справедливо и для жидкости, которое испытыва­ет на себе ускорение переносного движения. Под действием сил инерции переносного движения будет меняться положение свободной поверхности жидкости и поверхностей равного давления относительно стенок сосуда и относительно горизонтальной плоскости. Вид этих поверхностей целиком зависти от комбинации ускорений переносного движения и ускорения сил тяжести. В литературе состояние равновесия жидкости при наличии пе­реносного движения называется относительным покоем жидкости. Любые комбинации ускорений сводятся к двум возможным видам равновесия жидкости