2. Вязкость. Сдвиговая вязкость с точки зрения молекулярно-кинетической теории. Свойство прилипания жидкости. Закон вязкого трения Ньютона. Зависимость вязкости от температуры и давления.

Вязкость. Вязкость – это свойство жидкости сопротивляться сдвигу ее слоев. При течении жидкости вдоль твердой стенки слои жидкости, прилегающие к ней, тормозятся силами трения между слоями, то есть из-за вязкости (Рис. 1).

Согласно гипотезе Ньютона, подтвержденной экспериментально Н.П. Петровым, касательные напряжения при слоистом течении:

,

где – модуль поперечного градиента скорости [1/с],;

 – коэффициент динамической вязкости [Пас].

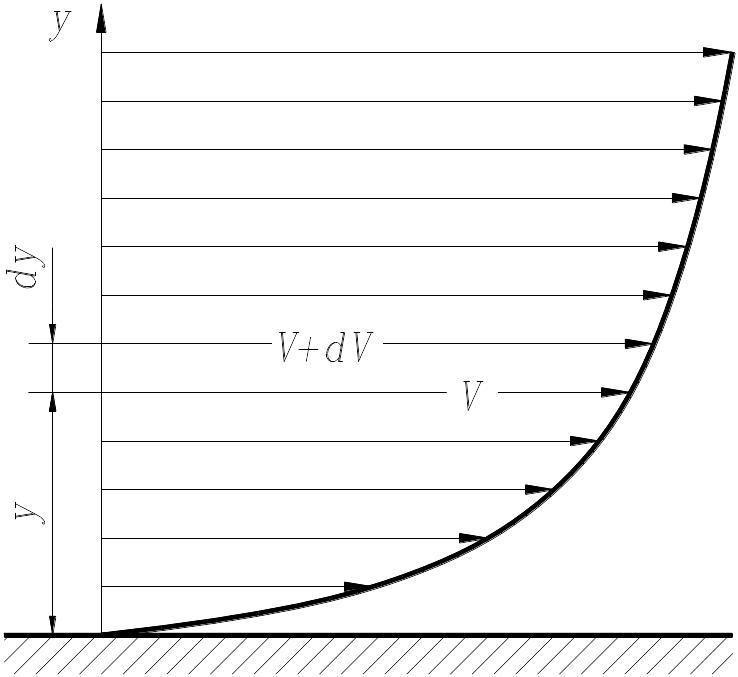
Рис. 1. Профиль скоростей при течении вязкой жидкости вдоль стенки

Из закона вязкого трения Ньютона следует, что касательные напряжения возможны только в движущейся жидкости. Если имеется градиент скорости еще и в направлении, нормальном плоскости рисунка, то следует записывать в формуле частную производную .

Кроме Пас используют такую единицу измерения, как Пуаз: 1П = 0,1 Пас.

Кроме коэффициента динамической вязкости, в технике широко используют коэффициент кинематической вязкости:

[м²/c].

С ростом температуры вязкость капельных жидкостей очень сильно падает (по экспоненте), а газов – растет по линейному закону. Например, при нагревании пресной воды от 0 до 100С коэффициент кинематической вязкости падает от 1,7910^-6 до 0,2910^-6 м²/с, то есть 6 с лишним раз. В этом же диапазоне температур вязкость минеральных масел изменяется в десятки и сотни раз. При отрицательных температурах вязкость масел резко возрастает.

Измеряют вязкость специальными приборами, называемыми вискозиметрами. Принцип действия этих приборов состоит в сравнении времени истечения заданного количества испытуемой и эталонной жидкостей через капилляр.

2. Ньютоновские и неньютоновские жидкости и их законы вязкого трения.

Следует сказать, что существуют жидкости, которые не подчиняются закону вязкого трения Ньютона. В качестве примеров можно назвать глинистые, цементные, известковые и коллоидные растворы, нефтепродукты и смазочные масла при температурах, близких к температуре застывания, краски, клеи, смолы, различные белки, жиры, суспензии крахмала, желатина и т.п. Это так называемые неньютоновские или аномальные жидкости. Для неньютоновских жидкостей зависимость касательных напряжений от поперечного градиента скорости может иметь один из следующих видов:

; .

Неньютоновские жидкости

Многокомпонентные жидкости как гомогенные, так и гетерогенные, в большей сте­пени, могут содержать в своём составе компоненты, значительно изменяющие вязкость жидкости, и даже кардинально меняющие саму физическую основу и природу внутренне­го трения. В таких жидкостях гипотеза вязкостного трения Ньютона (пропорциональность напряжений градиенту скорости относительного движения жидкости) неприменима. Со­ответственно такие жидкости принято называть неньютоновскими жидкостями.

2. Изолированная и замкнутая система. Химическое, динамическое, тепловое и термо­динамическое равновесие изолированной системы. Время релаксации. Равновесный процесс.

Смещение центра равновесия сил в пространстве называется релаксацией. Время, за которое происходит такое смещение, называется временем релаксации, t₀. При этом сме­щение центра равновесия осуществляется не постепенно, а скачком. Таким образом, время релаксации характеризует продолжительность «оседлой жизни» молекул жидкости. Если на жидкость будет действовать некоторая сила F, то при совпадении линии действия этой силы с направлением скачка, жидкость начнёт перемещаться. При этом необходимо вы­полнение дополнительного условия: продолжительность действия силы должна быть

больше длительности времени релаксации t₀, т.к. в противном случае жидкость не успеет

начать своё движение, и будет испытывать упругое сжатие подобно твёрдому телу. Тогда процесс движения жидкости будет характеризовать свойство текучести присущее практи­чески только жидким телам. Тела с такими свойствами относятся к категории жидких тел.