Основные понятия, определения и теоремы, которыми нужно владеть на экзамене

Сплошная среда

В гидромеханике рассматриваются макроскопические движения жидкостей и газов, а также силовое взаимодействие этих сред с твердыми телами. При этом, как правило, размеры рассматриваемых объемов жидкостей, газов и твердых тел оказываются несопоставимо большими по сравнению с размерами молекул и межмолекулярными расстояниями. Это естественно, поскольку межмолекулярные расстояния в жидкостях составляют всего см.

Указанные обстоятельства позволяют ввести гипотезу сплошности изучаемой среды и заменить реальные дискретные объекты упрощенными моделями, представляющими собой материальный континуум, т. е. материальную среду, масса которой непрерывно распределена по объему. Такая идеализация упрощает реальную дискретную систему и позволяет использовать для ее описания хорошо разработанный математический аппарат исчисления бесконечно малых и теорию непрерывных функций.

Капельная жидкость

Объектом изучения в гидравлике являются жидкости, чаще всего –так называемые капельные жидкости, то есть жидкости, которые в малых объемах под действием сил поверхностного натяжения приобретают сферическую форму. Иногда термин “жидкость” трактуют шире, включая в него, кроме капельных жидкостей, и газы.

Плотность(средняя и в точке)

Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости. Под плотностью жидкости понимается масса единицы объёма жидкости:

где: М - масса жидкости,

W - объём, занимаемый жидкостью.

В международной системе единиц СИ масса вещества измеряется в кг, объём жидко­го тела в м ³ ,

Напряжение (среднее и в точке';

Единичная поверхностная сила, называемая напряжением поверхностной силы, раскладывается на нормальные и касательные (тангенциальные) напряжения.

Нормальное напряжение называется гидромеханическим (а в случае покоя жидкости – гидростатическим) давлением, или просто давлением и обозначается p.

,

а при равномерном распределении поверхностной силы по площадке

.

Касательные напряжения (напряжения трения)  определяются аналогично

.

Точка жидкости

Течение и движение жидкости

Течение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным)

Вязкость (динамическая и кинематическая. сдвиговая и объемная)

Вязкость – это свойство жидкости сопротивляться сдвигу ее слоев. При течении жидкости вдоль твердой стенки слои жидкости, прилегающие к ней, тормозятся силами трения между слоями, то есть из-за вязкости (Рис. 1).

,

где – модуль поперечного градиента скорости [1/с],;

 – коэффициент динамической вязкости [Пас].

Кроме коэффициента динамической вязкости, в технике широко используют коэффициент кинематической вязкости:

[м²/c].

Вязкость - сопротивление действию внешних сил, вызывающих течение жидкости. Вязкость зависит от температуры и давления (>1МПа). Объемная вязкость - превращение механической энергии объемной деформации в теплоту.

Динамическая вязкость - характеризует силу внутреннего трения, возникающую на единице площади поверхности слоев жидкости. [Па × с]

Кинематическая вязкость - отношение динамической вязкости к плотности жидкости: n = mв / r [м2 / с]

Прилипание

Закон вязкого трения Ньютона

Из закона вязкого трения Ньютона следует, что касательные напряжения возможны только в движущейся жидкости. Если имеется градиент скорости еще и в направлении, нормальном плоскости рисунка, то следует записывать в формуле частную производную .

Температура (средняя и в точке)

Абсолютный ноль температуры

Абсолю́тный ноль температу́ры — это минимальный предел температуры, которую может иметь физическое тело. Абсолютный ноль служит началом отсчёта абсолютной температурной шкалы, например, шкалы Кельвина. По шкале Цельсия абсолютному нулю соответствует температура −273,15 °C.[1]

Считается, что абсолютный ноль на практике недостижим. Его существование и положение на температурной шкале следует из экстраполяции наблюдаемых физических явлений, при этом такая экстраполяция показывает, что при абсолютном нуле энергия теплового движения молекул и атомов вещества должна быть равна нулю, то есть хаотическое движение частиц прекращается, и они образуют упорядоченную структуру, занимая чёткое положение в узлах кристаллической решётки. Однако, на самом деле, даже при абсолютном нуле температуры регулярные движения составляющих вещество частиц останутся[1]. Оставшиеся колебания, например нулевые колебания, обусловлены квантовыми свойствами частиц и физического вакуума, их окружающего.[1]

Термодинамическое равновесие

Термодинамическое равновесие — состояние изолированной термодинамической системы, при котором в каждой точке для всех химических, диффузионных, ядерных, и других процессов скорость прямой реакции равна скорости обратной.

Термодинамическое равновесие можно делить на термическое, механическое и химическое равновесие, выделяя различные типы физических процессов, на которых достигнуто состояние равновесия.

Равновесный процесс

Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний.

Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений.

Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими.

Давление (гидростатическое, в идеальной и вязкой жидкости, абсолютное, избыточное, вакууметрическое. атмосферное, избыточ­ное гидродинамическое)

В общем случае поверхностная сила R, действующая на площадке S, направлена под некоторым углом к площадке, и ее можно разложить на две составляющие: нормальную F (перпендикулярную площадке) и тангенциальную T (направленную вдоль площадки). F называют силой давления, а T – силой трения.

Нормальное напряжение называется гидромеханическим (а в случае покоя жидкости – гидростатическим) давлением, или просто давлением и обозначается p.

,

Поверхность равного давления и плоскоть уровня

Поверхность, во всех точках которой давление одинаково называется поверхностью уровня. Как мы видим, эта поверхность – плоскость, параллельная свободной поверхности.

Несжимаемая и сжимаемая жидкость

Другой термодинамической характеристикой жидкости является сжимаемость.

Количественно сжимаемость оценивается изотермическим коэффициентом сжимаемости:

, (5)

где – удельный объем, . Жидкости, в отличие от газов, обладают малой сжимаемостью. Коэффициент сжимаемости большинства жидкостей лежит в пределах (Н/м²)^-1. Для всех жидкостей он уменьшается с возрастанием давления и возрастает с повышением температуры.

Объем жидкостей и газов изменяется не только при изменении давления, но и при изменении температуры. Как правило, жидкости и газы расширяются с повышением температуры, а плотность их при этом уменьшается. Исключение составляет вода, плотность которой возрастает при повышении температуры от 0 до 4 °С и достигает максимума при 4 °С. Такая аномалия объясняется особенностями молекулярного строения воды.

Идеальный (совершенный) газ

математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Различают классический идеальный газ (его свойства выводятся из законов классической механики и описываются статистикой Больцмана) и квантовый идеальный газ (свойства определяются законами квантовой механики, описываются статистиками Ферми — Дирака или Бозе — Эйнштейна).

Реальный газ - модель, при которой на сжимаемость газа при условиях близких к нормальным условиям существенно влияют силы взаимодействия между молекулами.

При изучении движения жидкостей и газов теоретическая гидравлика (гидромехани­ка) широко пользуется представлением о жидкости как о сплошной среде. Такое допуще­ние вполне оправдано, если учесть, что размеры пространства занимаемого жидкостью, во много раз превосходят межмолекулярные расстояния (исключением можно считать лишь разряженный газ). При изучении движения жидкостей и газов последние часто рассматри­ваются как жидкости с присущими им некоторыми особыми свойствами. Всвязи с этим принято различать две категории жидкостей: капельные жидкости (практически несжи­маемые тела, или собственно жидкости) и сжимаемые жидкости (газы).

Давление насыщенного пара

Давление насыщенного пара - давление пара, находящегося в замкнутом пространстве в термодинамическом равновесии с жидкостью того же химического состава. Кипение начинается при давлении насыщенного пара, равного внешнему давлению.

Закон Бойля-Мариотта

— один из основных газовых законов. Закон назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662, а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1676 году. Закон является частным случаем закона Менделеева-Клапейрона.

Закон Бойля-Мариотта гласит: при постоянной температуре и массе идеального газа произведение его давления и объёма постоянно:

, где:

p — давление газа

V — объём газа

Закон Гей-Люссака

Положение, что термический коэффициент расширения газа при постоянном давлении α с большой степенью точности одинаков для всех газов; поэтому

где vt — объем газа при температуре t по Цельсию, v0 — объем газа при 0°, причем α очень близко к 1/273 При точном значении α=1/273 закон справедлив для случая идеального газа; для реальных газов значения α несколько различны и зависят от температуры. Однако для атмосферного воздуха, далекого от состояния насыщения, при действительно наблюдаемых температурах 3. Г. Л. приложим с достаточной степенью точности.

Закон Шарля

ШАРЛЯ ЗАКОН, зависимость давления идеального газа от температуры при постоянных объеме и массе газа: при изменении температуры на 1 К давление изменяется на 1/273. Открыт французским ученым Ж. Шарлем в 1787, уточнен французским ученым Ж.Л. Гей-Люссаком в 1802.

Закон Клапейрона и

Клапейрона-Менделеева

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

 — давление,

 — молярный объём,

 — абсолютная температура,

 — универсальная газовая постоянная.

Уравнение Эйлера равновесия жидкости

Уравнение Эйлера для равновесия жидкости - совокупное дифференциальное уравнение равновесия жидкости под действием произвольных внешних сил.

Если dP1 и dP2 - внешние силы, то условие равновесия: dP1 - dP2 + dFx = 0; где dFx = dM × ax, dM = r × dW, dW = dx × dy × dz.

Сила гидростатического давления: dP = p × dw, если р1 и р2 - давление в точках приложения сил dР1 и dР2, то dР1 = p1 × dy × dz и dР2 = p2 × dy × dz. Если р = давление в центре тяжести, то: и .

Уравнение равновесия : , поскольку dy¹0 и dz¹0, то: . Аналогично для других координатных осей, получим уравнение Эйлера:

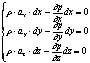
Сложив три уравнения получим: , при постоянной плотности жидкости: . ГМТ постоянного давления называется поверхностью равного давления или поверхностью уровня.

Основной закон гидростатики для несжимаемой жидкости

Диполь

Диполь — идеализированная система, служащая для приближенного описания распространения поля. Дипольное приближение основано на разложении потенциалов поля в ряд по степеням радиус-вектора и отбрасывании всех членов выше первого порядка. Полученные функции будут эффективно описывать поле в случае если

1. Размеры излучающей поле системы малы по сравнению с рассматриваемыми расстояниями, так что отношение характерного размера системы к длине радиус-вектора является малой величиной и имеет смысл рассмотрение лишь первых членов разложения потенциалов в ряд.

2. Член первого порядка в разложении не равен 0, в противном случае нужно использовать приближение более высокой мультипольности.

3. В уравнениях рассматриваются градиенты потенциалов не выше первого порядка.

Типичный пример диполя — два бесконечно близких заряда, равных по величине и противоположных по знаку. Поле такой системы полностью описывается дипольным приближением.

Уравнение неразрывности

Уравнение неразрывности - для стационарного течения жидкости - соотношение, связывающее: - плотность жидкости; - скорость жидкости в трубе; и - площадь поперечного сечения трубы. Живое сечение

Живым сечением потока называется поверхность в пределах потока, проведенная нормально к линиям тока. Если элементарные струйки проходят параллельно, то живое сечение потока будет плоским.

Средняя по живому сечению скорость

Уравнения Эйлера движения идеальной жидкости

уравнение Эйлера для движения идеальной жидкости в поле тяжести:

где — плотность жидкости, — давление в жидкости, — вектор скорости жидкости, — вектор напряжённости силового поля, — оператор набла для трёхмерного пространства.

Кавитация

образование в капельной жидкости пузырьков газа или пара. Происходит при падении давления в жидкости ниже давления насыщенного пара этой жидкости при данной температуре. Понижение давления происходит при высоких местных скоростях в потоке жидкости или при прохождении интенсивной акустической волны.

Интегралы Коши-Лагранжа, Эйлера, Бернулли, Громеко

Теорема Томсона

1. Циркуляция скорости замкнутого контура, образованного частицами жидкости, равна алгебраической сумме циркуляции по всем кривым, ограничивающим части поверхности S, охватываемой данным контуром s.

2. Ускорение циркуляции скорости замкнутого материального контура в жидкости равно циркуляции ускорения, т. е. криволинейному интегралу вдоль этого контура составляющей ускорения, направленной вдоль контура:

Теорема Лагранжа

Коэффициент давления

Гидродинамическая реакция

Сила сопротивления

это сила, препятствующая движению тел в жидкостях и газах. Лобовое сопротивления складывается из двух типов сил: сил касательного трения, направленных вдоль поверхности тела, и сил давления, направленных по нормали к поверхности.

Силы сопротивления удобно разделить на три категории: паразитное сопротивление, индуктивное сопротивление и волновое сопротивление. Каждый тип характеризуется своим собственным безразмерным коэффициентом сопротивления и определённой зависимостью от скорости движения.

Подъемная сила

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с законом Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Создавшаяся разница давлений и порождает подъёмную силу. Полная аэродинамическая сила — это интеграл от давления вокруг контура крыла.

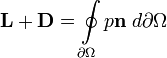
где:

L — это подъёмная сила,

D — это тяга,

- граница профиля,

p — величина давления,

n — нормаль к профилю

Согласно теореме Жуковского, величина подъёмной силы пропорциональна плотности среды, скорости потока и циркуляции скорости потока.

Парадокс Д'Аламбера-Эйлера

Д'Аламбера-Эйлера парадокс - положение гидродинамики, согласно которому при равномерном и прямолинейном движении тела произвольной формы, но конечных размеров внутри безграничной несжимаемой жидкости, лишенной вязкости, вихреобразований и поверхностей разрыва скоростей, результирующая сила сопротивления жидкости движению тела равна нулю [высказано Ж. Д'Аламбером в 1744 и Л. Эйлером (L.Euler) в 1745]. Парадокс Д'Аламбера-Эйлера строго доказан и для идеального совершенного газа, движущегося адиабатически. Физически отсутствие сопротивления объясняется тем, что при указанных условиях поток жидкости или газа должен замыкаться позади движущегося тела, причём жидкость оказывает на заднюю сторону тела воздействие, уравновешивающее воздействие (всегда имеющее место) на переднюю сторону.

В действительности тело при своём движении в жидкости или газе всегда испытывает сопротивление. Противоречие между действительностью и содержанием парадокса Д'Аламбера-Эйлера объясняется тем, что в реальной среде не выполняются те предположения, из которых строится доказательство парадокса. При движении тела в жидкости всегда проявляется вязкость жидкости, образуются вихри (в особенности позади тела) и возникают поверхности разрыва скорости. Эти термодинамически необратимые процессы и вызывают сопротивление движению тела со стороны жидкости.

Теорема Жуковского

Теоре́ма Жуко́вского — теорема о подъёмной силе тела, обтекаемого плоскопараллельным потоком идеальной жидкости или газа. Сформулирована Н. Е. Жуковским в 1904 году.

Формулировка теоремы:

Подъемная сила крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Направление действия подъемной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции.

В формульном виде:

, где

 — подъёмная сила,

ρ — плотность жидкости,

 — скорость потока жидкости на бесконечности,

 — циркуляция скорости (вектор направлен перпендикулярно плоскости профиля, направление вектора зависит от направления циркуляции),

l — длина отрезка крыла (перпендикулярно плоскости профиля).

Данная теорема явилась основой для построения современной теории крыла и гребного винта. Она даёт возможность рассчитать подъёмную силу крыла конечного размера, тягу гребного винта, нагрузку на лопатки турбины и так далее.

Для определения циркуляции скорости крылового профиля с острой задней кромкой удобно воспользоваться эмпирическим постулатом Жуковского — Чаплыгина.

Примечание. Можно вывести из принципа Бернулли и из формулы для сил давления .

Эффект Магнуса

Эффект Магнуса — физическое явление, возникающее при обтекании вращающегося тела потоком жидкости или газа. Образуется сила, воздействующая на тело и направленная перпендикулярно направлению потока. Это является результатом совместного воздействия различных физических явлений, таких как эффект Бернулли и образование пограничного слоя в среде вокруг обтекаемого объекта.

Вращающийся объект создаёт в среде вокруг себя вихревое движение. С одной стороны объекта направление вихря совпадает с направлением обтекающего потока и, соответственно, скорость движения среды с этой стороны увеличивается. С другой стороны объекта направление вихря противоположно направлению движения потока и скорость движения среды уменьшается. Таким образом, возникает разность давлений, порождающая поперечную силу от той стороны вращающегося тела, на которой направление вращения и направление потока противоположны, к той стороне, на которой эти направления совпадают. Такое явление часто применяется в спорте, см., например, специальный удар: топ-спин.

Эффект впервые описан немецким физиком Генрихом Магнусом в 1853 году.

Присоединенная масса

Присоединённая масса, величина, имеющая размерность массы, которая прибавляется к массе тела, движущегося неравномерно в жидкой среде, для учёта воздействия среды на это тело.

Свойство парности касательных напряжений

Гипотеза Стокса для обобщенного закон вязкого трения Ньютона

Уравнение движения жидкости в напряжениях

Геометрическое подобие

Геометрическое подобие, как известно из геометрии, предполагает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие тех поверхностей, которые ограничивают потоки, то есть подобие русел или каналов. При этом подобными должны быть не только русла в пределах изучаемого участка, но и непосредственно перед и за ними, так как они будут оказывать влияние на характер течения жидкости на изучаемом участке. Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим через k_L. Эта величина одинакова (idem) для подобных русел I и II:

.

Подобие во времени

Сходственные точки и моменты времени

Сходственные точки – это точки, отвечающие геометрическому подобию

Физическое подобие

Масштаб подобия

Необходимые условия динамического подобия

Экспериментальный путь изучения в принципе может учесть многие факторы, но он требует научно обоснованной постановки опытов, планирования эксперимента, ограничение его объема необходимым минимумом и систематизации результатов опытов. При этом часто опыты проводятся не с реальными явлениями, а с их моделями, так как параметры реальных явлений часто бывают неудобными для их изучения в лаборатории. Например, неудобно изучать в лабораторных условиях течение нефти в магистральном нефтепроводе из-за его большого диаметра, больших и очень мощных насосных установок, пожароопасности жидкости и т.п. Таким образом, необходимо принять обоснованные параметры модели. Эти задачи позволяет решить теория гидродинамического подобия. Гидродинамическое подобие складывается из трех составляющих: геометрического, кинематического и динамического подобия.

Сила давления на плоскую и криволинейную стенку

Как известно, сила характеризуется тремя параметрами:

– направлением:

– величиной;

– точкой приложения.

Давление в каждой точке стенки направлено по нормали к ней, следовательно, и равнодействующая сила давления будет перпендикулярна плоской стенке.

Ось 0x направим по линии пересечения стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно к этой линии в плоскости стенки.

Таким образом, полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление p_C в центре масс этой площади.

закон Архимеда, который гласит: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре масс объема погруженной части тела (центре водоизмещения).

F_в = p₀S_г +G

F_г = (p₀ + gh_C)S_в.

Закон Архимеда

Теорема Коши-Гельмгольца

Конвективное и местное ускорение

Хорошим примером такого рода может служить поток воды, перетекающий через плотину. Элементы жидкости, находящиеся выше плотины, движутся чрезвычайно медленно, по мере приближения к плотине ускоряются, а над ней проносятся очень быстро. Тем не менее поток в этом случае стационарный, так как скорость течения в каждой точке постоянна. Подобный вклад в ускорение частицы называется конвективным ускорением: частица испытывает его, когда перемещается с потоком из точки в точку. Вклад же в ускорение от изменения во времени скорости в данной точке называется местным ускорением.

Установившееся и неустановившееся течение

Установившимся называется течение, неизменное во времени, при котором давление и скорость являются только функциями координат, но не зависят от времени. Давление и скорость могут изменяться при перемещении частицы жидкости, но в данной неподвижной относительно русла точке давление и скорость во времени не изменяются:

В частном случае стационарное течение жидкости может быть равномерным, когда скорость каждой частицы не изменяется при изменении ее координат, и поле скоростей остается неизменным вдоль потока.

Неустановившимся называется течение жидкости, все характеристики которого (или некоторые из них) изменяются во времени в точках рассматриваемого пространства:

Принцип обратимости движения

В аэродинамике на основании принципа относительности классической механики сформулирован принцип обратимости: величина, направление и точка приложения аэродинамических сил не зависят от того, обтекается ли тело потоком воздуха, или же оно движется в неподвижном воздухе, и определяются только величиной и направлением относительной скорости тела и потока. Принцип обратимости позволяет вместо сил, действующих на реальный ЛА при его движении, рассмотреть силы, действующие на неподвижную модель ЛА, обтекаемую потоком воздуха.

Линия тока, вихревая линия

Рис. 16. Линия тока

Линия тока (Рис. 16) – это кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.

Вихревая линия

Линия в поле движения жидкости, касательная в каждой точке которой определяет направление вектора вихря скорости.

Трубка тока, вихревая трубка

ТРУБКА ТОКА в гидромеханике - трубка, составленная из линий тока, проходящих через точки небольшого замкнутого контура внутри движущейся жидкости.

Вихревая трубка

Замкнутая поверхность (трубка), состоящая из вихревых линий, проходящих через все точки некоторой замкнутой кривой в поле движения жидкости.

Дивергенция и циркуляция вектора скорости и вектора вихря

Соленоидальное поле и его свойства

Векторное поле назывется соленоидальным, если поток его через любую замкнутую поверхность равен нулю:

Это условие равносильно тому, что равна нулю его дивергенция:

Это условие выполняется тогда и только тогда, когда a имеет векторный потенциал A, то есть

Теорема Гаусса-Остроградского

Теорема Стокса

Первая и вторая теорема Гельмгольца о вихрях

Функция тока

Так как для несжимаемой жидкости поле скорости соленоидально, то у него существует векторный потенциал:

,

который можно считать векторной функцией тока.

Гидродинамическая сетка

Особые и критические точки в потоке

Источник (сток)

перемещение воды в виде потока

Плоский циркуляционный поток

Числа Ньютона, Фруда, Рейнольдса, Эйлера, Струхаля и соответствующие им критерии подобия

Это отношение называют числом Ньютона и обозначают Ne. Под силой F здесь понимается основная сила: сила давления, вязкости, тяжести или др. То есть это общий вид закона гидродинамического подобия.

где p – разность давлений или просто давление,

Eu – безразмерный критерий, число Эйлера.

Условие гидродинамического подобия потоков после деления на V ²L² примет вид:

где Re – безразмерный критерий, называемый числом Рейнольдса.

Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Рейнольдса, подсчитанных для сходственных сечений потоков.

Число Рейнольдса – основной критерий подобия напорных потоков. За характерный размер L при вычислении Re принимается поперечный размер потока, например, диаметр сечения (гидравлический диаметр).

Следовательно, условием гидродинамического подобия геометрически подобных потоков является равенство чисел Фруда. Из вывода видно, что число Фруда – это величина, пропорциональная отношению силы инерции к силе тяжести. Этот критерий важен при рассмотрении безнапорных течений в открытых руслах, для напорных течений его можно не учитывать.

где Fr – безразмерный критерий, число Фруда.

При рассмотрении течений, связанных с поверхностным натяжением (при распылении струи на капли), вводят критерий Вебера (We), пропорциональный отношению сил поверхностного натяжения к силам инерции:

При рассмотрении нестационарных периодических течений с периодом T (например, течение в трубопроводе, подсоединенном к поршневому насосу) вводят критерий Струхаля (Sh), учитывающий силы инерции от нестационарности, которые пропорциональны массе (L³) и ускорению (дV/дt), то есть V/T. Следовательно, условием гидродинамического подобия в этой ситуации будет

Автомодельность подобия

Автомодельность , особая симметрия физической системы, состоящая в том, что изменение масштабов независимых переменных, описывающих системы, может быть скомпенсировано преобразованием подобия (см. Подобия теория) др. динамических переменных. Автомодельность присуща многим физическим системам и существенно упрощает описание явлений в этих системах (напр., в аэромеханике и физике элементарных частиц). См. также Подобие физическое, Подобия критерии.

Пограничный слой

ПОГРАНИЧНЫЙ СЛОЙ - тонкая область течения вязкой жидкости (газа), которая образуется у поверхности обтекаемого ею твердого тела или на границе раздела двух потоков жидкости с различными скоростями, температурами или химическим составом. В пограничном слое скорость (температура, концентрация) резко изменяется; напр., скорость жидкости от нуля на поверхности обтекаемого тела, к которой она прилипает, возрастает в результате внутреннего трения до скорости основного потока.

Гидродинамический след

Внешний поток

Интеграл Бернулли для потока реальной жидкости

При переходе от элементарной струйки идеальной жидкости к потоку реальной жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению (Рис. 21), а также потери энергии (напора). И то, и другое является следствием вязкости жидкости.

Рис. 21. Распределение скоростей в реальном потоке

Это и есть уравнение Бернулли для потока реальной жидкости.

Отличий от уравнения Бернулли для элементарной струйки идеальной жидкости 3:

– есть слагаемое, учитывающее потери напора;

– использованы коэффициенты Кориолиса;

– использованы средние скорости потока в сечениях.

Коэффициент Кориолиса

 = – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока. Если умножить числитель и знаменатель этого выражения на /2, то становится понятно, что  – это отношение действительной кинетической энергии потока в данном сечении к кинетической энергии потока с тем же расходом и в том же сечении, но при равномерном распределении скоростей.

Формула Вейсбаха и Дарси-Вейсбаха

Местные потери напора определяются по формуле Вейсбаха

,

где V – средняя по сечению скорость в трубе, в которой установлено местное сопротивление; если диаметр трубы, а значит и скорость, изменяются, то в расчет принимают большую из двух скоростей;

_м – коэффициент местного сопротивления, который приближенно можно считать постоянным для данной формы местного сопротивления.

Формула для определения потерь напора на трение по длине примет вид:

.

Она носит название формулы Вейсбаха-Дарси, где  – коэффициент потерь на трение по длине или коэффициент Дарси.

Формулы Пуазенля, Блазиуса, Альтшуля, Шифринсона

В случае ламинарного течения с гармоническим изменением расхода по времени в закон Пуазейля, отражающий потери на трение по длине , надо ввести поправочный коэффициент

Для развитого турбулентного течения (4000 < Re < 10⁵) можно пользоваться формулой Блазиуса

или Конакова

Для этого режима , где d – диаметр трубы, можно применить формулу Альтшуля:

Эквивалентная шероховатость

Эквивалентная шероховатость – это искусственная равномерная шероховатость с такой высотой (диаметром) зерен при которой в области квадратичного сопротивления (где зависит только от шероховатости и не зависит от ) значение коэффициента равно его значению при естественной шероховатости.

Формула Торичелли, приведенный напор

ТОРРИЧЕЛЛИ ФОРМУЛА - скорость жидкости, вытекающей из отверстия в стенке сосуда: , где h - расстояние от оси отверстия до поверхности жидкости, g - ускорение силы тяжести. Выведена Э. Торричелли в 1641.

Коэффициенты сжатия, скорости и расхода при истечении жидкости через отверстие или насадок

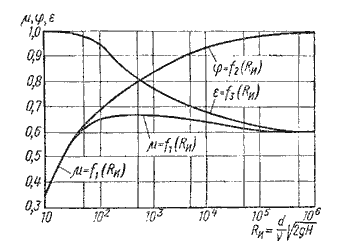
Критический напор при истечении жидкости через насадок

36