43. Парадокс д'Аламбера-Эйлера. Причины возникновения силы сопротивления.

Д'Аламбера-Эйлера парадокс - положение гидродинамики, согласно которому при равномерном и прямолинейном движении тела произвольной формы, но конечных размеров внутри безграничной несжимаемой жидкости, лишенной вязкости, вихреобразований и поверхностей разрыва скоростей, результирующая сила сопротивления жидкости движению тела равна нулю [высказано Ж. Д'Аламбером в 1744 и Л. Эйлером (L.Euler) в 1745]. Парадокс Д'Аламбера-Эйлера строго доказан и для идеального совершенного газа, движущегося адиабатически. Физически отсутствие сопротивления объясняется тем, что при указанных условиях поток жидкости или газа должен замыкаться позади движущегося тела, причём жидкость оказывает на заднюю сторону тела воздействие, уравновешивающее воздействие (всегда имеющее место) на переднюю сторону.

В действительности тело при своём движении в жидкости или газе всегда испытывает сопротивление. Противоречие между действительностью и содержанием парадокса Д'Аламбера-Эйлера объясняется тем, что в реальной среде не выполняются те предположения, из которых строится доказательство парадокса. При движении тела в жидкости всегда проявляется вязкость жидкости, образуются вихри (в особенности позади тела) и возникают поверхности разрыва скорости. Эти термодинамически необратимые процессы и вызывают сопротивление движению тела со стороны жидкости.

44. Теорема Жуковского о подъемной силе. Эффект Магнуса. Возникновение подъем­ной силы на крыле.

Жуковского теорема, теорема о подъёмной силе, действующей на тело, находящееся в плоскопараллельном потоке жидкости или газа. Согласно этой теореме, подъёмная сила, действующая на тело в потоке жидкости или газа, обусловлена связанными с обтекаемым телом вихрями (присоединёнными вихрями), причиной возникновения которых является вязкость жидкости. Наличие этих вихрей приводит к обтеканию крыла потоком с отличной от нуля циркуляцией скорости. Сформулирована Н. Е. Жуковским в 1904.

  Если установившийся плоскопараллельный потенциальный поток (см. Потенциальное течение) несжимаемой жидкости набегает на бесконечно длинный цилиндр перпендикулярно его образующим, то на участок цилиндра, имеющий длину вдоль образующей, равную единице, действует подъёмная сила Y, равная произведению плотности (среды на скорость v потока на бесконечности и на циркуляцию Г скорости по любому замкнутому контуру, охватывающему обтекаемый цилиндр, т. е. Y =vГ. Направление подъёмной силы получается из направления вектора скорости на бесконечности поворотом его на прямой угол против направления циркуляции. Ж. т. справедлива и при дозвуковом обтекании профиля сжимаемой жидкостью (газом). Для звуковой и сверхзвуковых скоростей обтекания Ж. т. в общем виде не может быть доказана.

  Ж. т. легла в основу современной теории крыла и гребного винта. С помощью Ж. т. могут быть вычислены подъёмная сила крыла конечного размаха, тяга гребного винта, сила давления на лопатку турбины и компрессора и др.

В предыдущем параграфе мы рассмотрели силу, возникающую при обтекании тела потоком,— силу сопротивления воздуха, направленную по скорости потока. Однако так бывает только в тех случаях, когда обтекаемое тело вполне симметрично относительно потока. Если же тело несимметрично по форме или несимметрично расположено относительно потока, то сила, действующая на тело, направлена под углом к потоку. Такова, например, сила, действующая на крыло летящего горизонтально самолета со стороны встречного потока воздуха. На рис. 341 показан разрез («профиль») крыла и действующая на него сила F. Эта сила направлена под большим углом к горизонту. Ее можно разложить на две составляющие: вертикальную F1 и горизонтальную F2. Вертикальную составляющую (перпендикулярную к направлению потока) называют подъемной силой. Именно благодаря Рис. 341. Разложение силы F, действующей на крыло самолета, на подъемную силу F1 и лобовое сопротивление F2 Рис. 342. При вращении цилиндра скорость увлекаемого воздуха с одной стороны складывается со скоростью потока (вверху), а с другой — вычитается (внизу) возникновению подъемной силы при обтекании тел оказалось возможным создание летательных аппаратов тяжелее воздуха: подъемная сила поддерживает самолет в воздухе. Горизонтальную составляющую, направленную по потоку, называют силой лобового сопротивления. Возникновение лобового сопротивления нами уже разобрано. Теперь мы должны пояснить, каким образом возникает подъемная сила, направленная перпендикулярно к потоку. Для этого мы сначала рассмотрим обтекание вращающегося цилиндра равномерным потоком воздуха (рис. 342). В этом случае движение воздуха сравнительно просто и направление сил легко определить. При своем вращении цилиндр увлекает прилегающие слои воздуха; в результате окружающий воздух получает, кроме поступательного движения, еще и вращение вокруг цилиндра. В тех местах, где скорости поступательного и вращательного движений складываются, результирующая скорость воздуха превосходит скорость потока, набегающего на цилиндр; с противоположной стороны цилиндра скорости вычитаются и результирующая скорость меньше, чем скорость потока вдали от цилиндра. Рис. 343 изображает получающееся распределение линий тока. Там, где скорость больше, линии тока расположены гуще. Но из закона Бернулли мы знаем, что в тех местах, где скорость больше, давление понижено, и наоборот. Следовательно, с двух сторон на цилиндр действуют неравные 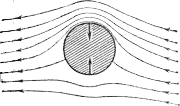Рис. 343. 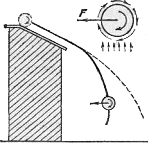Линии тока проведены гуще с той стороны вращающегося цилиндра, где скорость потока больше; давление с этой стороны меньше Рис. 344. Эффект Магнуса на падающем вращающемся цилиндре силы; их результирующая, направленная перпендикулярно к потоку, и является подъемной силой. Подъемная сила, перпендикулярная к потоку, возникает при вращении не только цилиндра, но и любого другого тела. Возникновение силы, перпендикулярной к потоку, при обтекании вращающегося тела называется эффектом Магнуса. Эффект Магнуса был впервые обнаружен при изучении полета вращающихся артиллерийских снарядов: подъемная сила, действующая со стороны встречного потока воздуха, отклоняет снаряд от линии прицела; это отклонение должно быть учтено при точной стрельбе. В меньшем масштабе эффект Магнуса можно наблюдать на летящем футбольном или теннисном мяче, который отклоняется в сторону, если при ударе он получил вращение. Эффект Магнуса можно легко обнаружить при помощи опыта, изображенного на рис. 344. Легкий бумажный цилиндр, скатываясь с наклонной доски, отклоняется при падении от обычной траектории (штриховая линия) и движется по более крутой линии (сплошная линия). Встречный поток воздуха направлен относительно цилиндра вверх, а цилиндр вращается по часовой стрелке; поэтому возникающая подъемная сила F направлена справа налево. Возникновение подъемной силы связано с наличием кругового движения потока воздуха около обтекаемого тела; это круговое движение, налагаясь на общий поток, создает разницу в скоростях потока с двух сторон тела, благодаря чему и создается разность давлений, обусловливающая подъемную силу. Круговое движение потока вокруг тела называется циркуляцией. В эффекте Магнуса циркуляция, а следовательно, и подъемная сила возникают благодаря вращению цилиндра. В других случаях циркуляция может быть вызвана не вращением тела, а иными причинами. Для возникновения подъемной силы важно только, чтобы поток, обтекающий тело, имел циркуляцию. Тогда распределение скоростей всегда будет такое, что образующаяся разность давлений создаст силу, направленную перпендикулярно к потоку.

45, Гидродинамические реакции при неустановившемся движении тела. Инерционная гидродинамическая сила. Присоединенная масса, присоединенный момент инерции массы и присоединенный статический момент массы.

46. Матрица напряжений движущейся вязкой жидкости. Свойство парности касатель­ных напряжений.