12. Предельные теоремы.

235. Дать определение характеристической функции.

Характеристической функцией случайной величины называется функция от вещественной переменной:

, если F(x) – ф-ция распределения, то

236. Перечислить основные свойства характеристической функции.

237. Как характеристическая функция связана с плотностью вероятности?

238. Записать формулы для вычисления характеристической функции дискретных случайных величин.

239. Записать формулы для вычисления характеристической функции непрерывных случайных величин.

240. Как вычислить начальные моменты с использованием характеристической функции?

241. Как определяются кумулянты случайной величины?

- кумулянт к-того порядка.

242. Как определяются кумулянтные коэффициенты случайной величины?

Капец полный нигде такого нету ;%№:4325

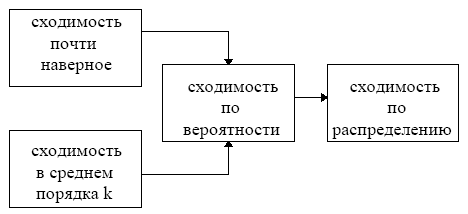
243. Перечислить основные виды сходимости случайных величин.

Почти наверное, по вероятности, в среднеквадратическом, по распределению.

244. Что такое сходимость с вероятностью единица?

Последовательность случайных величин ξn сходится к случайной величине ξ почти наверное, или с вероятностью 1, если

245. Что такое сходимость по вероятности?

Последовательность случайных величин ξn сходится к случайной величине ξ по вероятности, если для любого ε>0

246. Что такое среднеквадратическая сходимость?

Последовательность случайных величин ξn сходится к случайной величине ξ в среднеквадратическом, если

247. Что такое сходимость по распределениям?

Пусть P{ξ<x}=F(x) и P{ξn<x}=Fn(x). Тогда говорят, что ξn сходится к ξ по распределению, если

248. Как связаны различные виды сходимости?

Из сходимости почти наверное следует сходимость по вероятности, но из сходимости по вероятности не следует сходимость почти наверное. Из сходимости в среднеквадратическом следует сходимость по вероятности. Из сходимости по вероятности следует сходимость по распределению.

249. В чём заключается центральная предельная теорема?

Данная теорема определяет условия, при которых возникает случайная величина с нормальным законом распределения. Различные формы центральной предельной теоремы различаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых X1, X2, …, Xn. Чем жестче эти условия, тем легче доказывается теорема; чем они шире, тем труднее доказательство.

250. Сформулировать центральную предельную теорему.

если случайная величина X представляет собой сумму очень большого числа независимых случайных величин, влияние каждой иэ которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному.

251. Сформулировать интегральную теорему Муавра-Лапласа.

Для любых вещественных x < y при имеет место сходимость

252. Сформулировать локальную теорему Муавра-Лапласа.

Пусть Р(А) — вероятность события А. Тогда вероятность того, что в условиях схемы Бернулли событие А при n испытаниях появится точно m раз, выражается приближенной формулой Лапласа:

253. Сформулировать теорему Пуассона.

Пусть , так, что . Тогда для любого вероятность получить k успехов в n испытаниях схемы Бернулли с вероятностью успеха стремится к величине

254. Дать определение безгранично делимой случайной величины.

Случайная величина называется безгранично делимой, если для любого целого числа n ее можно представить в виде суммы n независимых одинаково распределенных слагаемых.

255. Привести примеры безгранично делимых случайных величин.

Хз, проявляем фантазию.

256. Записать каноническое представление Колмогорова характеристической функции безгранично делимой случайной величины.

Колмогорова не застали, спросить не смогли, записи не сохранились.

257. Какие законы распределения называются устойчивыми? Привести примеры.

Если сумма любого числа случайных величин с некоторым распределением после соответствующей перенормировки имеет то же самое распределение, что и каждое слагаемое, такой закон распределение называют устойчивым. Пример – нормальный закон распределения.