2.7. Испытание на растяжение. Определение характеристик прочности

Рассмотрим испытание на растяжение пластичных и хрупких материалов, так как с помощью таких испытаний определяются наиболее важные механические характеристики материалов.

Д ля испытания изготавливают образцы круглого ( рис. 2.10,а) или прямоугольного ( рис. 2.10,б) поперечного сечения. Концевые части образцов имеют головки для закрепления в захватах испытательной машины (рис.2. 10).

Рис. 2.10

На рабочей части образца выделяется расчетная длина, которая согласована с размером диаметра образца. Обычно испытывают образцы длинные l₀ =10d и короткие l₀ =5d .

По результатам испытания строится диаграмма растяжения в координатах Р-∆l, или σ – ε.

Здесь Р – растягивающее усилие.

∆l - изменение расчетной длины,

- напряжение,

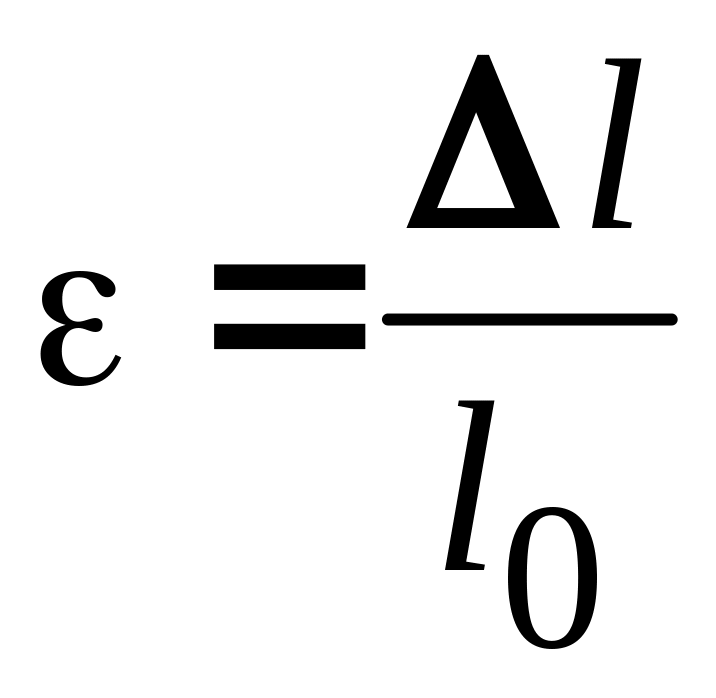- относительная продольная деформация.

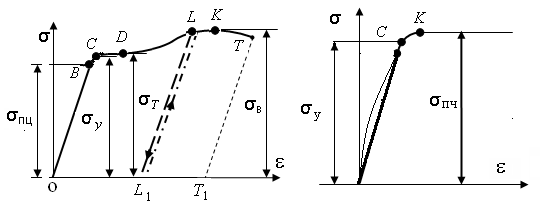
Диаграмма растяжения малоуглеродистой стали представлена на рис.2.11,а. На начальном этапе деформирования (участок ОВ) зависимость между напряжением и деформацией линейна, справедлив закон Гука .

Наибольшее напряжение, до которого соблюдается закон Гука, называется пределом пропорциональности –- . На диаграмме это соответствует точке В.

(а) (б)

Рис. 2.11

Напряжение, соответствующее точке С, называется пределом упругости - .

Предел упругости- это наибольшее напряжение, до которого остаточная деформация не обнаруживается.

Образец, будучи разгружен по достижению предела упругости, полностью восстанавливает первоначальные размеры. Значения и близки друг к другу, и обычно различием между ними пренебрегают. При дальнейшем повышении напряжений наряду с упругой деформацией происходит накопление пластической деформации. При этом у малоуглеродистой стали деформации начинают расти практически при постоянной нагрузке. Этот эффект называют текучестью. На диаграмме наблюдается площадка текучести CD. Пределом текучести σ_т называется напряжение, при котором образец заметно деформируется без увеличения нагрузки.

Для ряда конструкционных сталей на диаграмме растяжения отсутствует площадка текучести. В таком случае вводится понятие условный предел текучести, который обозначают .

За условный предел текучести принимают наименьшее напряжение, при котором остаточная деформация составляет 0,2%.

При дальнейшем деформировании образца наступает зона упрочнения. Этому соответствует восходящий участок DK. Если разгрузить образец из любой точки , расположенной на этом участке, процесс разгрузки описывается прямой параллельной участку ОВ. При этом остаточная деформация характеризуется отрезком . При повторном нагружении (штрих пунктирная линия на диаграмме) повышается первоначальный предел пропорциональности. Явление, при котором происходит повышение упругих свойств материала в результате предварительного пластического деформирования, называется наклепом. В ряде случаев наклеп полезен и его создают искусственно.

Точка K соответствует наибольшему усилию, которое выдержал образец. В этот момент происходит потеря устойчивости равномерной пластической деформации и образуется местное сужение в виде шейки. Площадь поперечного сечения изменяется и дальнейшее деформирование происходит при падении нагрузки.

Отношение максимальной силы, которую способен выдержать образец, к его первоначальной площади поперечного сечения называется временным сопротивлением или пределом прочности . При напряжении, соответствующем точке Т, происходит разрыв образца.

Основными характеристиками прочности материалов, используемыми в практических расчетах являются:

предел пропорциональности 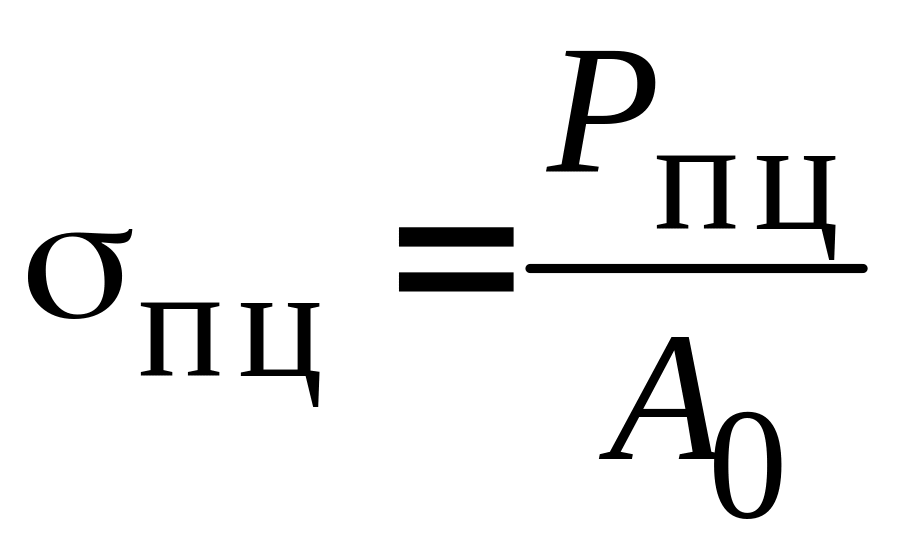, (2.12)

предел упругости , (2.13)

предел текучести , (2.14)

временное сопротивление или

предел прочности . (2.15)

Для малоуглеродистой стали, имеющей площадку текучести, например, для Ст2 эти характеристики следующие:

Диаграмма растяжения хрупких материалов представлена на рис. 2.11,б. Разрыв образца происходит при незначительном удлинении и без образования шейки. Диаграмма не имеет выраженного прямолинейного участка. Однако, в связи с незначительностью отклонения от линейности, деформации на начальной стадии растяжения определяют, пользуясь законом Гука.

По результатам испытания можно определить предел упругости и предел прочности .
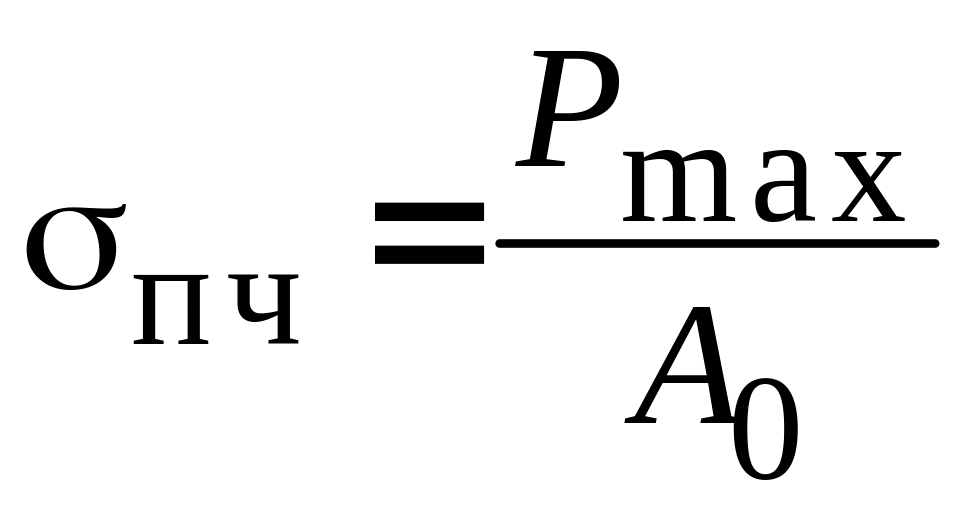