7.3 Деформации при объемном напряженном состоянии. Обобщенный закон Гука

Изучая осевое растяжение, мы выяснили, что относительная продольная деформация связана с напряжением:

, (7.15)

а относительная поперечная деформация с продольной

. (7.16)

Рассмотрим деформацию элемента тела размерами a,b,c по граням которого действуют главные напряжения и .

Д

Рис. 7.8

еформацию в направлении от обозначим .

Деформация в направлении от равна Деформация в направлении от ,равна .

Аналогично могут быть определены деформации и в направлении действия двух других главных напряжений.

Сведем расчетные соотношения в таблицу.

Таблица 7.1

В напр. От

Выражая полную деформацию, получаем

в направлении действия

в направлении действия (7.17)

в направлении действия

Воспользовавшись соотношением (7.15), получаем обобщенный закон Гука при трехосном напряженном состоянии:

(7.18)

7.4 Потенциальная энергия упругой деформации

Энергия, накапливаемая в объеме материала при его упругом деформировании, называется потенциальной энергией упругой деформации U.

Значение потенциальной энергии упругой деформации определяется из закона сохранения энергии.

Процесс восстановления размеров и формы тела после снятия внешней нагрузки при упругом деформировании свидетельствует о том, что работа внешних сил, производимая на упругих перемещениях, численно равна энергии упругой деформации:

В случае статического нагружения, в пределах действия закона Гука, работа внешних сил при растяжении выражается площадью диаграммы деформирования (рис.7.9)

. (7.19)

Рис. 7.9

Энергию, накапливаемую в единице объема, называют удельной потенциальной энергией деформации :

(7.20)

В общем случае под действием приложенных внешних нагрузок имеет место изменение формы и размеров (объема)

.

Объемная деформация, как показывают экспериментальные исследования, остается упругой и исчезает после снятия нагрузки. Деформация формы может быть как упругой, так и пластической. Так как разрушению предшествует пластическое деформирование, то основную часть накапливаемой потенциальной энергии составляет энергия формоизменения

. (7.21)

Анализ напряженно деформированного состояния в общем случае позволяет сформулировать основные характеристики напряженно-деформированного состояния.

К ним относятся:

1. главные напряжения

2. главные деформации

3. максимальное касательное напряжении

4. удельная потенциальная энергия формоизменения .

7.5 Проверка прочности в общем случае сложного напряженного состояния. Теории прочности

Прочность оценивают путём сопоставления вычисленных главных напряжений в опасной точке с допускаемыми напряжениями. Допускаемые напряжения могут быть определены лишь из опыта. Поэтому механические испытания материала должны производиться в тех же условиях, в которых работает материал реальных конструкций. Реализация этого требования для простого (линейного) напряженного состояния не составляет труда. Испытание на растяжение позволяет установить величины и предельных (опасных) напряжений, и допускаемых.

Так как количество соотношений главных напряжений очевидно неограниченно, то для получения прочностных характеристик экспериментальным путем понадобилось бы бесчисленное множество отдельных опытов, а так же специальное оборудование.

Другой путь решения задачи о прочности в общем случае напряженного состояния заключается в установлении критерия прочности. При этом сопоставляют сложное напряженное состояние с линейным.

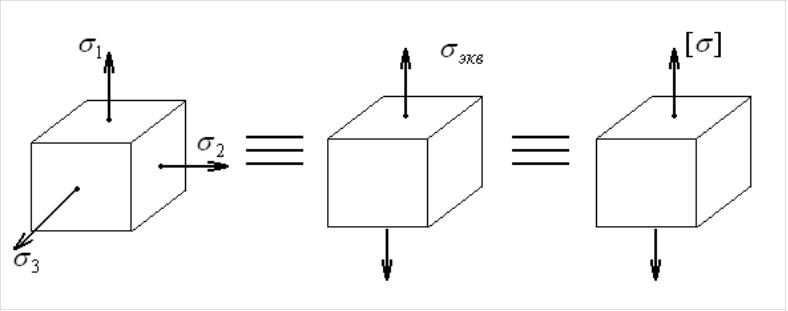
(а) (б) (в)

Рис.7.10

Задача заключается в том, чтобы, зная главные напряжения , выразить эквивалентное напряжение . Величина эквивалентного напряжения зависит от выбранного критерия эквивалентности по прочности.

Высказывается гипотеза о преимущественном влиянии на прочность того или иного параметра, характеризующего напряженно деформированное состояние. Гипотезы или теории прочности принято нумеровать в порядке их исторического возникновения.

Первая теория прочности – теория наибольших нормальных напряжений.

Согласно первой теории прочности два напряженных состояния считаются равнопрочными (эквивалентными по прочности), если равны между собой наибольшие нормальные напряжения.

Так как , наибольшее нормальное напряжение . Приводя сложное напряженное состояние (рис 7.10, а) к эквивалентно-му (рис 7.10, б) получаем условие эквивалентности . Условие прочности записывается следующим образом

. (7.22)

Здесь – допускаемое напряжение на растяжение.

Если имеет место всестороннее сжатие меньше нуля, то первая теория прочности требует соблюдения условия прочности по сжимающим напряжениям

(7.23)

Вторая теория прочности – теория наибольших линейных деформаций.

По второй теории прочности предполагается, что решающее влияние на прочность оказывает наибольшее относительное удлинение e₁. Оно имеет место в направлении действия наибольшего главного напряжения .

(7.24)

Условие прочности (7.25)

ил и

(7.26)

Если , , меньше нуля, то по второй теории прочности потребуется проверка прочности не только по наибольшему относительному удлинению, но и по наибольшему относительному укорочению.

(7.27)

Первая и вторая теории прочности экспериментально подтверждаются при хрупком разрушении, которое характеризуется появлением разрывов, трещин, что характерно для группы хрупких материалов.

Третья теория прочности – теория наибольших касательных напряжений.

В основу этой теории положено представление о большей опасности пластического разрушения. За критерий прочности принимается наибольшее касательное напряжение

(7.28)

Для эквивалентного состояния , следовательно

или

Условие прочности по третьей теории прочности

(7.29)

Третья теория прочности применима лишь к материалам, равнопрочным в отношении растяжения и сжатия (этому условию отвечают пластичные материалы)

Четвертая теория прочности – энергетическая.

За критерий прочности по этой теории принимается удельная потенциальная энергия формоизменения.

Выражая энергию формоизменения через главные напряжения и деформации, приходим к определению эквивалентного напряжения

(7.30)

В таком случае условие прочности по четвертой теории прочности

(7.31)

Четвертая теория прочности применима так же, как и третья, к материалам, равнопрочным в отношении растяжения и сжатия. Представим запись условия прочности для плоского напряженного состояния. Выражая главные напряжения через напряжения, действующие на произвольных площадках, получаем

;

;

.