4.4 Моменты сопротивления

Характеристики сечений, которые часто встречаются в расчётных соотношениях на прочность, часто записываются в форме . Эти соотношения рассматриваются как вспомогательные геометрические характеристики, называемые моментами сопротивления.

Осевые моменты сопротивления сечения , полярный момент сопротивления . Здесь − расстояние до точки сечения, максимально удалённой от рассматриваемой оси или полюса.

Моменты сопротивления простейших сечений

Рис. 4.7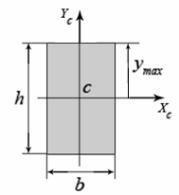

Прямоугольник

(4.13)

К

Рис. 4.8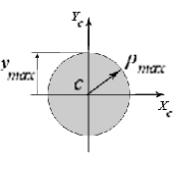

руг

. (4.14)

Полярный момент сопротивления

Рис. 4.9

(4.15)

Составное сечение

Момент сопротивления такого сечения относительно оси как вспомогательная характеристика вычисляется следующим образом:

.

Момент сопротивления этого же сечения относительно оси

. (4.16)

4.5 Зависимость между моментами инерции относительно параллельных осей, одна их которых центральная

Рассмотрим сечение, центральная ось которого . Параллельно оси на расстоянии а проходит ось (рис. 4.10). Момент инерции относительно оси , параллельной центральной , равен моменту инерции относительно центральной оси . плюс произведение площади фигуры на квадрат расстояния между осями.

Для доказательства сказанного следует выразить момент инерции относительно оси как интегральную функцию

.

З

Рис. 4.10

десь -момент инерции относительно центральной оси, статический момент сечения относительно центральной оси , который равен нулю,

-площадь сечения.

В результате получается:

, аналогично . (4.15)

4.6 Главные оси и главные моменты инерции сечения

Главными называются центральные оси, относительно которых осевые моменты инерции сечения достигают экстремальных значений, а центробежный момент инерции равен нулю.

Сформулированному положению отвечает система осей, проходящих через центр тяжести сечения, если хотя бы одна из них является осью симметрии.

П

Рис. 4.11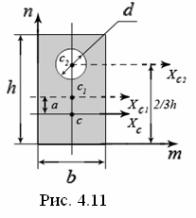

ример

Определить положение главных осей и величины главных моментов инерции сечения прямоугольной формы с отверстием, центр тяжести которого находится на расстоянии от основания прямоугольника, при . ( рис.4.11)

Определяем положение центра тяжести сечения в системе вспомогательных осей m-n. В силу симметрии координата

Координата может быть определена с использованием понятия статического момента площади относительно оси m- .

Отсюда следует

. (4.16)

Здесь ;

.

Расстояние между осями и обозначим .

Расстояние между осями и обозначим .

.

На основании (4.8) .

Для определения главного момента инерции сечения необходимо воспользоваться теоремой о параллельном переносе осей, в соответствии с которой

.

Здесь ;

.

Определяем главный момент инерции сечения . Ось − главная центральная ось сечения совпадает с главными центральными осями прямоугольника и отверстия .

.

Геометрические характеристики стандартных прокатных профилей, таких, как двутавр, швеллер, уголки равнобокие и неравнобокие, приводятся в технических справочниках, а также (выборки из ГОСТа) приведёны в учебниках по сопротивлению материалов.