Билет 2

1

М-ичная АМП (S(t), A(t), сигнальное созвездие, функциональная схема).

При М-ичной амплитудной манипуляции амплитуда передаваемого сигнала скачкообразно изменяется в соответствии с символами передаваемого сообщения:

Здесь A(t) может принимать M возможных амплитуд, соответствующих M=2^m возможным m-битовым символам (m-разрядность одного передаваемого символа). На рисунке дана геометрическая иллюстрация формируемого ансамбля амплитудно-манипулированных сигналов при объеме алфавита М = 2, М = 4, М = 8, d = 2.

Двоичные символы, создаваемые источником дискретных сообщений, предварительно кодируются кодом Грея. В результате соседние сигнальные точки отображают двоичные последовательности, отличающиеся одним двоичным символом.

Функциональная схема устройства формирования М-АМП сигнала приведена на рисунке

Преобразованная последовательность входных битов преобразователем уровня DA1 поступает на вход демультиплексора DD1, который разделяет входную последовательность на m-последовательностей. Блок задержек DD2 выравнивает по времени эти последовательности, блок расширителя DD3 увеличивает длительность каждого до значения длительности канального символа T_c=mT_b . Аналого-цифровым преобразователем DD2 формируется амплитуда синфазной составляющей I, квадратурная составляющая при этом равна нулю. На выходе перемножителя DA3 получаем М-АМП сигнал.

2

Итеративные коды. Показать принцип кодирования.

Данные коды характеризуются наличием двух или более систем проверок внутри каждой кодовой комбинации. Запишем все информационные разряды блока, подлежащего передаче, в виде таблицы (рис. 2.3).

Каждая строка этой таблицы кодируется каким-либо кодом, а затем кодируется каждый столбец, причем не обязательно тем же кодом. Символы, расположенные в правом нижнем углу таблицы, получаются в результате проверки проверочных символов. Они могут быть построены на основе проверки по строкам и тогда будут удовлетворять проверке по столбцам, и наоборот.

В качестве примера рассмотрим итерированные коды (рис. 2.4) с одной проверкой на четность для каждого столбца и строки.

			1	0	0	1	1	1
Информационные символы	Проверочные символы по строкам		1	1	0	0	1	1
			1	0	0	0	1	0
			1	1	1	1	1	1
			1	9	9	9	9	1
Проверочные символы по столбцам	Проверка проверок		0	0	1	1	0	0
			1	0	0	1	0	0

Рис. 2.3. Расположение символов итеративного кода

Рис. 2.4. Итеративный код

Итерированный код позволяет исправить все одиночные ошибки, так как пересечение строки и столбца, содержащих ошибку, однозначно указывает ее место. Передача комбинации итеративного кода обычно происходит по строкам последовательно, от первой строки к последней.

Свойства итеративного кода полностью определяются параметрами итерируемых кодов, в зависимости от которых итеративный код может быть как систематическим, так и несистематическим, как разделимым, так и неразделимым. Длина кодовой комбинации, число информационных разрядов и минимальное кодовое расстояние итеративного кода очень просто выражаются через соответствующие параметры этих кодов:

,

где - параметры итерируемых кодов; - кратность итерирования.

Таким образом, простейший итеративный код, образованный путем проверок на четность (нечетность) строк и столбцов, обладает минимальным кодовым расстоянием и поэтому позволяет обнаруживать все ошибки кратности до 3.

3

Детекторы АМ-сигнала с использованием нелинейной характеристики. Спектр сигнала до и после детектирования.

По своему назначению детектирование является процессом, обратным процессу модуляции. На вход детектора подается модулированное колебание, содержащее только высокочастотные составляющие: несущее колебание и боковые частоты. На выходе детектора появляется напряжение с низкочастотным спектром передаваемого сообщения. Следовательно, детектирование сопровождается трансформацией частотного спектра и не может быть осуществлено без применения нелинейных элементов. В качестве таких элементов используются полупроводниковые диоды, полевые и биполярные транзисторы.

Предположим, что вольт-амперная характеристика (ВАХ) нелинейного элемента описывается выражением i = a+bu +cu².

Если на входе действует АМ-сигнал:

, то ток

С пектр сигнала до (а) и после (б) детектирования показан на рисунке

Как видно из рисунка, в низкочастотной части спектра, кроме составляющей с частотой модулирующего сигнала , есть еще постоянная составляющая и вторая гармоника модулирующего сигнала, которая приводит к искажениям.

Во избежание искажений при детектировании необходимо, чтобы детектор обладал линейно-ломаной ВАХ.

Спектр АМ-сигнала при демодуляции с использованием линейной характеристики

В составе спектра нет искажающих сигнал гармоник низкой частоты.

Процесс детектирования состоит из выпрямления АМ колебаний, в результате которого образуются импульсы несущей с огибающей, имеющей форму колебания передаваемого сообщения и выделения из этих импульсов исходного сигнала путем фильтрации высокочастотных составляющих спектра импульсов.

3.1 Амплитудная модуляция. Выводы выражения. Временные диаграммы. Спектр сигнала при модуляции одним тоном.

Изменение амплитуды носителя по закону передаваемого сообщения называется амплитудной модуляцией (АМ).

Если модулирующий сигнал (полезное сообщение) описывается выражением

А Носитель

То амплитуда носителя будет изменяться по закону C(t).

Выражение для АМ сигнала

k – коэффициент пропорциональности

Подставив предыдущие получим

Заменив произведение косинусов, получим

где – коэффициент глубины амплитудной модуляции, или просто коэффициент модуляции.

Для того чтобы модуляция была без искажений, коэффициент модуляции не должен быть больше единицы, т.е. . При наступает перемодуляция.

Из временной диаграммы для АМ сигнала следует, что

Если модулирующее сообщение содержит n гармонических составляющих (а не одну гармонику), т.е. характеризуется полосой частот от _min до _max (рисунок 2.2,б) и описывается выражением

то спектр сигнала передачи кроме основной составляющей будет содержать нижнюю (НБП) и верхнюю (ВБП) боковые полосы

Выражение для АМ-сигнала в данном случае имеет вид:

3.2 Декодирование циклических кодов по методу дописывания нулей. Показать на примере F*(x) = 1000110, S = 1, P(x) = x³+x+1.

Сначала определяется остаток , соответствующий наличию ошибки в старшем разряде. Если ошибка произошла в следующем разряде, то такой же остаток получится в произведении принятого многочлена на 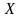, т.е. . Это служит основанием для следующего приема.

Вычисляем как остаток от деления на . Далее делим принятую комбинацию на и получаем . Если , то ошибка в старшем разряде. Если нет, то дописываем нуль, что равносильно умножению на , и продолжаем деление. Номер искаженного разряда (отсчет слева направо) на единицу больше числа приписанных нулей, после которых остаток окажется равным .

Пример

Вычисляем как остаток от деления на , получаем . Далее делим на , отмечая полученные остатки :

Для достижения равенства пришлось дописать три нуля. Это означает, что ошибка произошла в четвертом разряде, т.е. исправленная кодовая комбинация будет иметь вид

.

3.3 Детекторы АМ-сигнала с использованием линейно-ломаной характеристики (рис. 5.7; 5.8). Спектр сигнала до и после детектирования (рис. 5.9).

Детектирование колебаний заключается в восстановлении модулирующего сигнала, который в неявной форме содержится в модулированном высокочастотном колебании. По своему назначению детектирование является процессом, обратным процессу модуляции. В тех случаях, когда требуется подчеркнуть это, наряду с термином “детектирование” (“обнаружение”) применяют термин “демодуляция” колебаний.

На вход детектора подается модулированное колебание, содержащее только высокочастотные составляющие: несущее колебание и боковые частоты. На выходе детектора появляется напряжение с низкочастотным спектром передаваемого сообщения. Следовательно, детектирование сопровождается трансформацией частотного спектра и не может быть осуществлено без применения нелинейных элементов. В качестве таких элементов используются полупроводниковые диоды, полевые и биполярные транзисторы.

Во избежание искажений при детектировании необходимо, чтобы детектор обладал линейно-ломаной ВАХ, представленной на рисунке 5.7 или 5.8.

Спектр сигнала после детектирования показан на рисунке 5.9.

В составе спектра нет искажающих сигнал гармоник низкой частоты. Поэтому детектор с ВАХ, представленной на рисунке 5.7 или 5.8, называют линейным.

Процесс детектирования состоит из выпрямления АМ колебаний, в результате которого образуются импульсы несущей с огибающей, имеющей форму колебания передаваемого сообщения и выделения из этих импульсов исходного сигнала путем фильтрации высокочастотных составляющих спектра импульсов.

4. 1.КФМП (S(t) ,Q(t), сигнальное созвездие КФМП-4, функциональная схема).

Квадратурная фазовая манипуляция (КФМП). При ДФМП один канальный символ переносит один передаваемый бит. Однако, как уже отмечалось выше, один канальный символ может переносить большее число информационных бит. Например, пара следующих друг за другом битов может принимать четыре значения: {0, 0}{0, 1}{1, 0}{1, 1}.

Здесь (t) может принимать значения из множества:

где – произвольная начальная фаза.

В дальнейшем вместо четырех канальных символов или четырех радиосигналов будем говорить о единственном радиосигнале, комплексная амплитуда которого может принимать четыре указанных значения, представленных рисунке 4.10 в виде сигнального созвездия.

Каждая группа из двух битов представляется соответствующим фазовым углом, все фазовые углы отстоят друг от друга на 90°. Можно отметить, что каждая сигнальная точка отстоит от действительной или мнимой оси на =45°.

Последовательность передаваемых битов 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0,… разбивается на две подпоследовательности нечетных 1, 1, 0, 1, 0, 1, … и четных 0, 1, 0, 0, 1, 0,… битов с помощью демультиплексораDD1.

Биты с одинаковыми номерами в этих подпоследовательностях образуют пары, которые удобно рассматривать как комплексные биты; действительная часть комплексного бита есть бит нечетной подпоследовательностиI, а мнимая часть Q– бит четной подпоследовательности. При этом биты нечетной последовательности в синфазной ветви задерживаются на время Tб устройством DD2. Далее длительность каждой последовательности уменьшается до значения 2Tб расширителями DD3 и DD4.

Полученные таким способом комплексные биты преобразуются в комплексную последовательность прямоугольных электрических импульсов длительностью 2Тб со значениями +1 или -1 их действительной и мнимой частей, которые используются для модуляции несущего колебания exp{ }. В результате получается КФМП-4 радиосигнал.

4.2 Декодирование циклических кодов по методу вычисления остатка. Показать на примере F*(x) = 1000110, S = 1, P(x) = 1011.

Заключается в следующем:

1) вычисление остатка. Принятую кодовую комбинацию делят на P(x), и если остаток R(x)=0, то комбинация принята без искажений. Наличие остатка свидетельствует о том, что комбинация принята искаженной. Дальнейшая процедура исправления рассматривается ниже;