38. Найти теплоемкость квантового кристалла в гармоническом приближении. Определить теплоемкость такого кристалла в пределах низкой и высокой температур.

В квантовой теории теплоемкости гармонического кристалла вместо классического выражения для плотности тепловой энергии:

необходимо пользоваться общим квантово-механическим результатом.

(1)

- энергияi-го стационарного состояния кристалла.

Полная энергия равна сумме отдельных нормальных мод:

(2)

Чтобы вычислить вклад колебаний решетки во внутреннюю энергию, подставим в общую формулу (1) выражение для энергетических уровней (2). Для облегчения вычислений введем величину:

чтобы найти f, заметим, что если разложить произведение

то каждому значению энергии Е будет соответствовать в точности один член в разложении. Отдельные сомножители в произведении представляют собой сходящиеся геометрические прогрессии, суммирование которых дает

тогда плотность внутренней энергии будет равна (дифференцируем f):

где - среднее значение числа описывающего степень возбуждения нормальной модыksпри температуре Т (среднее число фононов типаksв состоянии теплового равновесия).

Итак для плотности энергии гармонического кристалла получаем:

При Т -> 0 третье слагаемое обращается в 0. Удельная теплоемкость:

теплоемкость зависит от конкретного вида спектра частот нормальных мод.

Семинар № 10.

41. Найти теплоемкость кристалла в моделях Эйнштейна и Дебая.

В

квантовой теории гармонического кристалла теплоёмкость имеет вид:

(интеграл по первой зоне Бриллюэна)

В

— В модели Дебая

модели Дебаявсе ветви колебательного спектра заменяются тремя ветвями с одним и тем же линейным законом дисперсии

Кроме того, в формуле для С_Vвместо интеграла по первой зоне Бриллюэна берётся интеграл по сфере радиусомk_D , который выбирается так, чтобы сфера содержала ровноNразрешённых волновых векторов (N– число ионов в кристалле). Поскольку объем вk-пространстве, приходящийся на один волновой вектор, равенэто означает чтои следовательноk_D определяется соотношением. После таких упрощений формула для С_Vимеет вид:

дебаевская частота - дебаевская температура -

Сделаем следующую замену переменных в формуле для С_V:

После соответствующих преобразований получим

В модели Эйнштейна мы пренебрегаем акустическими ветвями в фононном спектре (для акустических ветвей используется модель Дебая, а для оптических - Эйнштейна).

;

В Эйнштейновском приближении каждая оптическая ветвь вносит в тепловую энергию вклад

Поэтому если имеется pтаких ветвей, то в удельной теплоемкости появится дополнительный член:

42. Выразить импульс Дебая kd через радиус эквивалентной сферы для 1-го электрона, вычислить его значение для щелочных металлов.

;

следовательно Дебаевский импульс выраженный через r_s :

Вычисления:

43. Рассмотреть высоко- и низкотемпературный предел теплоемкости в модели Дебая.

-теплоемкость в теории Дебая

приполучается интеграл приблизительно от нуля, до нуля () поэтому его можно разложить в ряд:

и следовательно С_Vпри малых температурах пропорциональна Т.

При интегрируем примерно от нуля до бесконечности и следовательно С_Vпри больших температурах пропорциональна Т³.

Семинар № 11.

44. Вывести уравнение состояния твёрдого тела в модели Грюнайзена и

1) получить зависимость давления Р от величины ;

2) показать, что в гармоническом приближении ;

3) ввести параметр Грюнайзена и связать его с коэффициентом линейного расширения;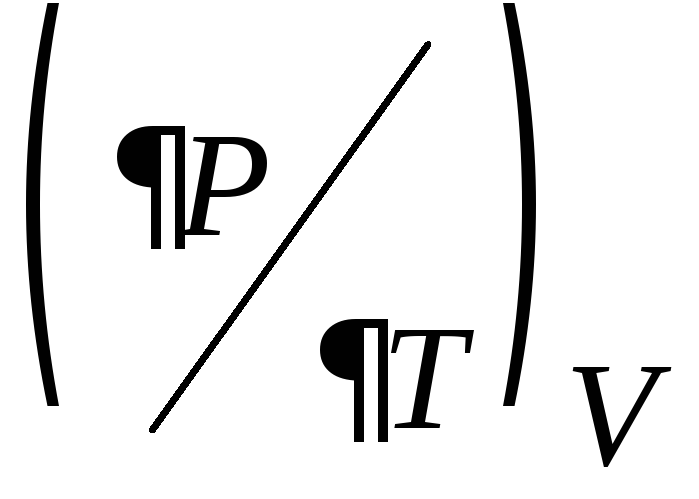

4) найти связь между параметром Грюнайзена и параметрами ангармонического потенциала.

Из воспоминаний о термодинамике:

В гармоническом приближении:

Покой нам только снится

Где последнее слагаемое даёт вклад фононной энергии:

Давление зависит от температуры лишь поскольку частоты нормальных мод зависят от равновесного объёма кристалла. Но в гармоническом приближении:

где - смещение ионов относительно своих положений в точках

- вторая производная от потенциальной энергии по смещению, не зависит от,

значит на частоты нормальных мод не влияет изменение равновесного объёма (для одномерных осцилляторов)

Коэффициент линейного теплового расширения вводится как

модуль всестороннего сжатия:

подставляем сюда выражение для давления из полученного уравнения состояния кристалла:

введём параметр Грюнайзена для моды :

полный параметр Грюнайзена:

, т.е. вклад моды определяется её теплоёмкостью

В итоге получаем: , если γ – число, то α ведёт себя как теплоёмкость.