22. Показать, что в теории Блоха k – квазиимпульс.

Для действительного импульса имеем:

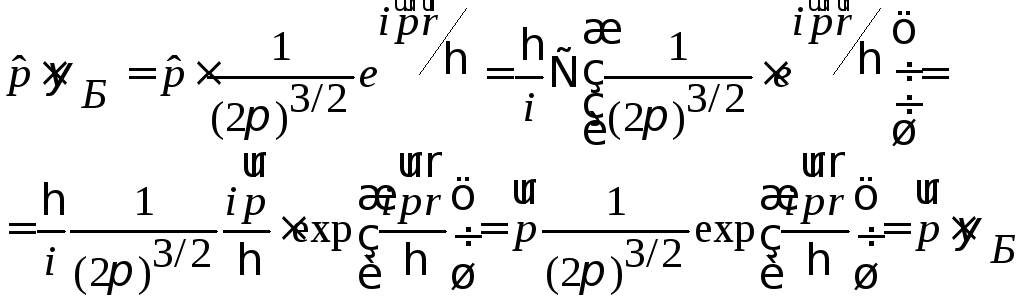
Для имеем:

Семинар № 6.

23. Рассмотреть движение электронов в периодическом потенциале вида:

;

(Модель Кронига-Пенни). Найти энергетические зоны.

Решения ур. Шредингера в двух областях:

ψ₁=A₁exp(iαx)+A₂exp(-iαx), где α=(2mE)^1/2/ћ

Ψ₂=B₁exp(βx)+ B₂exp(-βx), где β=[2m(U₀-E)]^1/2

В точке -a- в.ф. должна быть непрерывной вместе со своей производной:

Ψ₁(a)= Ψ₂(b), , Ψ₂(0)= exp(-ikb)Ψ₁(b) ,

{ A₁e^iαa + A₂e^-iαa = B₁e^βa + B₂ e^-βa

iα[A₁e^iαa-A₂ e^-iαa]= β[B₁e^βa- B₂ e^-βa]

B₁+B₂=e^-ikb[A₁e^iαb+A₂ e^-iαb]

β(B₁-B₂)=e^-ikbiα[A₁e^iαb+A₂ e^-iαb] }

Выражая в данной системе A₁иA₂, получим однородную СЛАУ относительно В₁и В₂ , детерминант которой должен быть=0.

В итоге получим:

(4β/iα)(1+e^2ikb)+e^ikb(4β/iα)[-sinα(b-a)sh βa{(β²-α²)/ α β }-2chβacos α(b-a)]=0

1+ e^2ikb-2e^ikb[{(β²α²)/ α β} shβa sinα(b-a)+chβa cosα(b-a)]=0

(1/2)(e^-ikb+ e^ikb)=[-||-]

cos(kb)= [(β²-α²)/ 2α β] sh(βa) sin[α(b-a)]+ch(βa) cos[α(b-a)]

Данное равенство определяет связь энергии с волновым числом -к-, которое зависит от а, b,U₀.

27. Рассмотреть движение е- в периодическом потенциале вида Дираковской решётки. Найти энергетические зоны.

Решение уравнения Шредингера: ψ₁=Aexp(ikx)+Bexp(-ikx), 0xa

В соседнем интервале :

Получим условия для функции и ее производной в точке x=a:

при :

В итоге получаем систему:

Получили однородную СЛАУ относительно Aи В , детерминант

которой должен быть=0.

Из последней формулы следует, что зоны разрешённых значений энергий определяются следующим неравенством:

Семинар №7.

29. Показать, что в случае, когда движение электрона в кристалле можно рассматривать как распространение плоской волны , квант соответствует импульсу. Показать, что если на кристалл действует внешнее поле, то скорость изменения импульса в зависимости от времени такова, что электрон может рассматриваться как частица, обратная масса которой является тензорной величиной, имеющей компоненты

Решение.

В рассеивающей среде

,,

Для волнового пакета

Для плоской волны мы имеем соотношения:

для импульса , для энергии.

Если электрон находится во внешнем поле , то

,

Значит, реакция на действие внешней силы такова, как будто электрон обладает импульсом .

Сравним это уравнение с уравнением механики , получим:

30. Рассмотреть различия между металлом, полупроводником и диэлектриком с точки зрения структуры их энергетических зон. Схематически изобразить поверхность Ферми двумерного кубического кристалла, который имеет небольшое число носителей эффективных зарядов на атом (полуметалл).

Решение.

Рис.1Картина изменения энергии в зоне вдоль одного направления вk-пространстве

Если число валентных электронов на атом является достаточным заполнения состояния так, чтобы уровень Ферми (пунктир) проходил как в случаях 1 или 2, то вещество – металл. Если уровень Ферми проходит как в случае 3, т.е. находится внутри запрещённой зоны, вещество является диэлектриком.

Для того, чтобы кристалл был диэлектриком, уровень Ферми должен оказаться в запрещённой зоне для всех . Для большинства диэлектриков существует большая энергетическая щель между валентной зоной и зоной проводимости. Если энергетическая щель узкая, то при тепловом возбуждении электроны могут преодолеть её сами, или при помощи примесей (электроны могут занимать энергетические уровни примесных атомов внутри щели), и попасть в зону проводимости. В этом случае вещество обладает полупроводниковыми свойствами.

Для металлов в k-пространстве можно изобразить поверхность постоянной энергии на границе Ферми.

В данном случае, карманы – совокупность занятых состояний во второй зоне Бриллюэна (заштрихованная область В) – в то же время приводят к образованию «пустых» карманов – совокупности незанятых состояний (область А). Оба типа карманов образуются обычно вблизи границ зоны, где ход изменения энергии часто отличается от параболического, и, где эффективная масса отличается от массы свободного электрона. Вследствие близости карманов к запрещённым областям энергии, число эффективных носителей тока в таких случаях невелико.