11. Имитационные модели (общее описание).

Имитационное моделирование – это способ получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемом объекте. Составными частями имитационной модели являются описания: элементов, образующих систему; структуры системы, т.е. совокупности связей между элементами; свойств среды, в которой функционирует исследуемая система. Указанная информация в целом имеет логико-математический характер и представляется в форме совокупности алгоритмов, описывающих функционирование исследуемой системы. Программа, построенная на основе этих алгоритмов, позволяет получить информацию о поведении исследуемой системы.

Имитационные модели применяются, если математическая модель аналитически не решается, или если нас не устраивает точность расчёта аналитической модели, которая может быть неудовлетворительной из-за погрешностей, получаемых в результате грубых допущений. Исходя из этого, чаще всего применяются именно имитационные модели, в которых Q-схемы воспроизводятся без ограничений.

Имитационные модели имеют следующие достоинства:

• теоретически неограниченная универсальность;

• потенциально высокая точность;

• многопараметричность;

• высокая адекватность.

К недостаткам имитационной модели относятся сравнительно высокая сложность и трудоемкость.

12. Примеры математических моделей (анал. И имитационных).

Матем модель (аналитич, алгебраич).

В целях упрощения учтем только ср знач пар-ов системы и сделаем допущение, что все заявки одинаковы, поступают ч/з 7с и обслуж за 3с. Модель станет статичной, детермин-ной и ее решение описыв-ся след соотношениями:

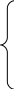
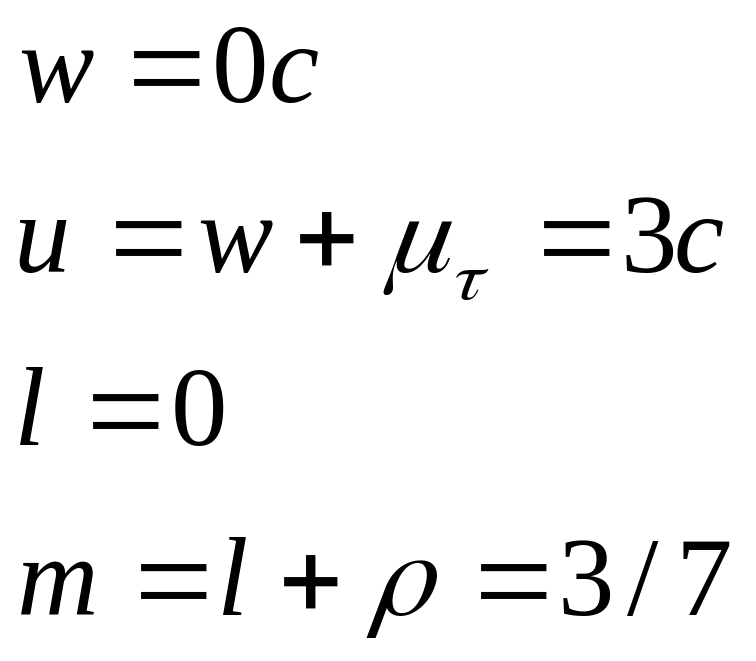
Матем модель (аналитич, вероятност). Учтем случ. хар-р поступл-я и обслуж-я заявок. Законы и заменим теоретическими, для кот известно аналитич решение. Сохраним лишь их совпадение на уровне матем-их ожиданий. Будем считать, что заявки во вх потоке распредел по закону Пуассона, а время обслуж t подчиняются экспон-ому закону. Соотв-но ср. интенсивность потока заявок и ср. скорость обслуж остаются прежними. При таких допущениях моделью системы будет СМО типа М/М/1 и можно использ известные формульные решения.

Матем модель (имитацион)Учтем в модели все знания об объекте, в том числе реал законы поступлен. и обслуж-я заявок. Модель будет строиться как динамич, вероятностная. Модельное время меняется дискретно, алгоритм продвиж-я модельного времени - событийный. Стр-ра модели представл. на рис15, где модули М1 и М2 выполн. роль генераторов.М1 генерирует последов-сть сл. чисел , подчин. закону распредел , а М2 имитирует длительн. времени обсл. заявок t в соотв. с заданным законом распредел .МЗ имитирует функцион-е объекта, реагируя на происх-щие в нем события и изменяя его состояния, собирает инфу о прошлых, текущем и будущих состояниях объекта. М4 выполняет статистику обраб. накопленных результ и вычисл хар-ки, а М5 управляет моделью и ходом моделирования.

Алгоритм работы модели на уровне модулей включ. след. этапы: ввод исходных данных (пар-ов среды и объекта.