89. Моделирование узловых характеристик объекта на основе замкнутых сетей мо.

---опред. коэфф. загрузок отдельных СМО ( например, для одноканальных СМО --- используя выражения для расчёта коэфф. загрузки, определяют интенсивности потоков заявок в каждую СМО.

90. Общая методика моделирования объекта на основе разомкнутых сетей мо.

Рассчитываем интенсивности потоков на входе в каждую СМО. . Указанные состояния образуют систему линейных уравнений (кол-во N) с N неизвестными. Решая уравнения, находим все . Попутно, если не были заданы, рассчитываем их. .

Рассчитываем вероятности состояний.

Рассчитываем узловые характеристики, начиная с загрузки.

Если СМО одноканальная, используем соответствующие формулы для одноканальной системы, если многоканальная – для многоканальной.

Можно использовать вероятности состояний.

Расчёт системных характеристик.

Суммарная длина очередей ,

Общее количество заявок. ,

Среднее время обслуживания. ,

Среднее время ожидания. .

91. Общая методика моделирования объекта на основе замкнутых сетей мо.

В замкнутых сетях начинается расчёт с коэффициентов передач. Используются аналогичные соотношения из N уравнений с N переменными.

Рассчитываем вероятности всех состояний.

Рассчитываем узловые характеристики. .

Вычислив загрузки, определим оставшиеся узловые характеристики. . Рассчитываем . Для любой СМО рассчитываем .

Рассчитываем все оставшиеся системные характеристики.

92. Предельные оценки характеристик стохастических сетевых моделей

Предельные (асимптотические) характеристики объекта можно получить, построив асимптотическую модель. Допустим, что выполнение всех заявок в сети спланировано идеальным образом. Т.е. заменим случайные законы поступления и обслуживания заявок в сети детерминированными с сохранением средних значений их параметров i, i, и i. Это приведет к тому, чго модель будет характеризоваться максимальной производительностью₀, и соответственно минимальным временем пребывания (обработки) заявок в сети U_­0.

В сети можно выделить два режима работы: до насыщения и после насыщения. В режиме насыщения к сети появится хотя бы один полностью загруженный узел с коэффициентом загрузки р_s =1, т.е. "узкое место" и пусть;

М* - число заявок, переводящих сеть в режим насыщения. Рассмотрим каждый режим в отдельности.

В режиме до насыщения при любом числе заявок в сети удовлетворяющем условию М < М* заявки могут быть "идеально" спланированы и обрабатываются так, как если бы в сети была только одна заявка Соответственно все j =0, время пребывания заявки в сети постоянно и равно длительности обработки одной заявки 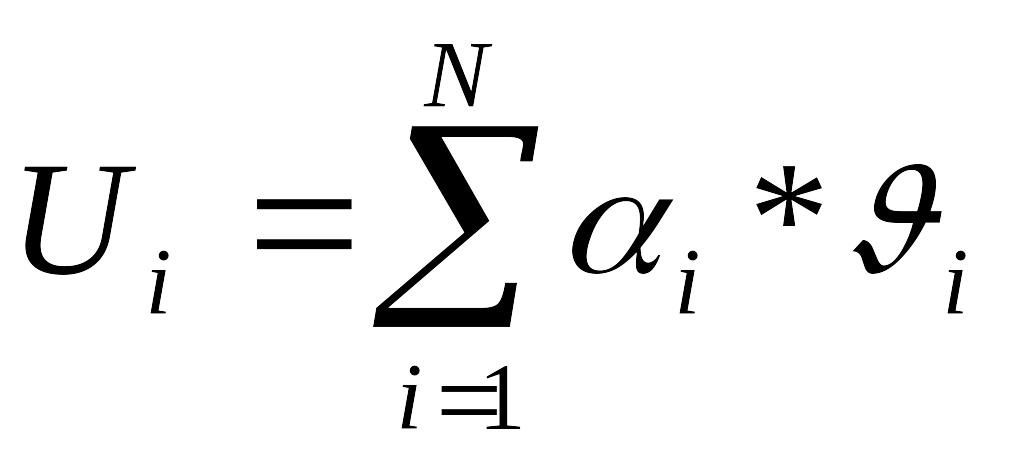, а производительность сети определится по закону Литтла

Если увеличивать число заявок в сети М, то наступит момент, когда хотя бы один из узлов окажется полностью загруженным и станет "узким местом" Сеть войдет в режим насыщения, дальнейшее увеличение числа заявок в сети не будет вести к росту ее производительности, достигнутой в точке М = М* и будет определяться параметрами (пропускной способностью) "узкого места".В режиме насыщения (М > М*) производительность сети постоянна и равна ₀(M)=M/U₀=M*/U₀ (при М=М*), а время пребывания заявки в с определится по закону Литтла