83.Экспоненциальные сети мо.

Сеть массового обслуживания называется экспоненциальной поток заявок является простейшим, а законы обслуживания заявок – экспоненциальными.

Простейшим называется поток, который распределен по Пуассоновскому закону:

где:

– вероятность того, что за время  в систему поступит n заданий;

- время поступления задания на обслуживание;

- параметр закона поступления заданий (скорость поступления).

В теории систем массового обслуживания существует утверждение, что при экспоненциальном законе распределения поступления и обслуживания заявок, система будет нагружена максимально.

84. Расчёт интенсивностей потоков и , сама сеть в соотв. Фициент мкнутой сети.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000коэффициентов передач сетей мо.

иллюстрируется на рисунке 1. Вх. поток в каждой СМО складывается из суммы вых. потоков всех СМО сети, взвешенных вероятностью перемещения заявок с их выходов на вход рассм. СМО.

Соотв. для каждой i-ой СМО получаем уравнение:

Для сети будет получена система ,

( где ) из N линейных уравнений с N неизвестными,

решение которой даст искомые значения .

Коэфф. передачи каждой СМО рассчитывают по формуле .

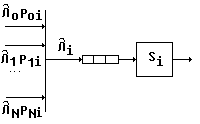
Рис 1. Расчёт потоков заявок.

85. Расчёт вероятностей состояний разомкнутых сетей мо.

Здесь нормирующий коэфф. равен 1, сама сеть в соотв. с теоремой Джексона распада-ется на ряд изолированных СМО, поэтому вероятности состояний 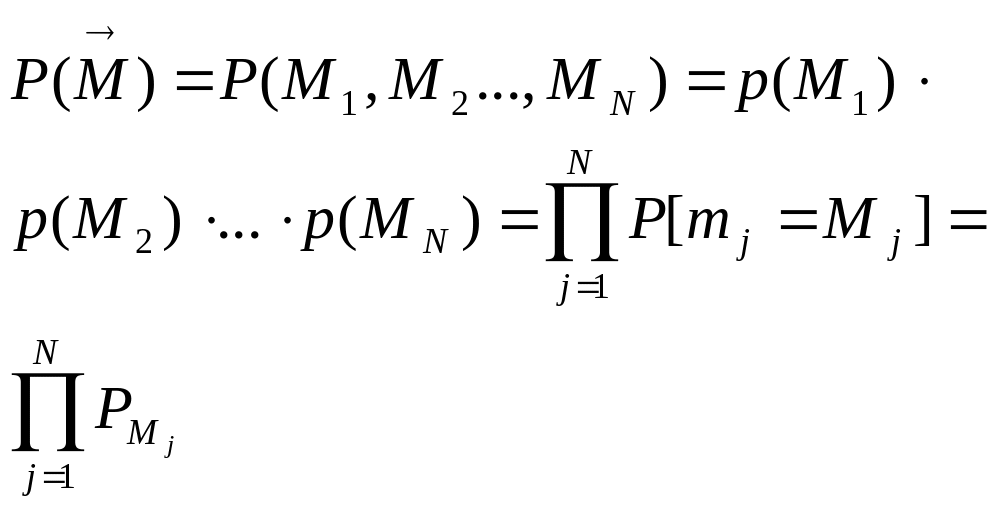и

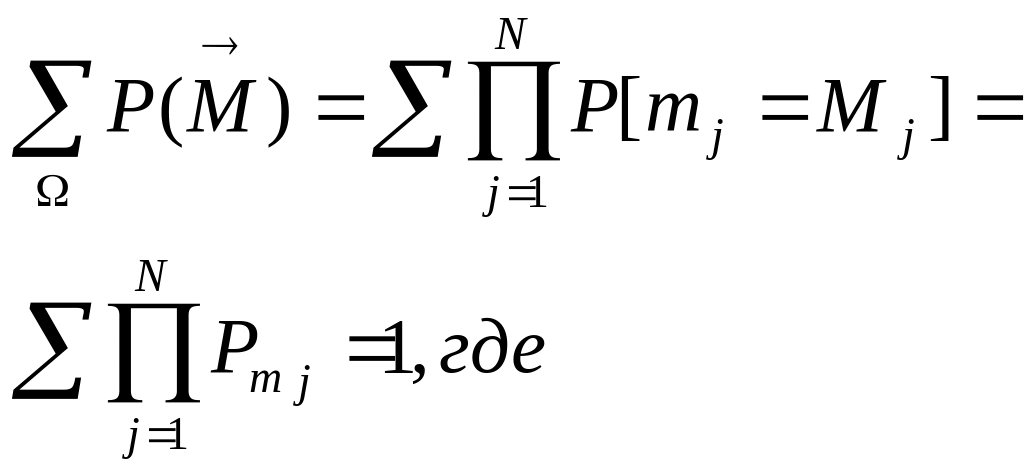
- вероятность состояния j-ой СМО (вероятн. того, что в ней находиться ровно M_j заявок.

86. Расчёт вероятностей состояний замкнутых сетей мо.

Здесь как и для разомкнутой сети вероятности состояний определяются через вероятно-сти составляющих её СМО. Из-за отсутствия в сети состояний, не удовл. условию

Из этого выражения опред. нормирующий множитель

. Соотв. вероят-ность состояний

Если сеть состоит только из одноканальных СМО, то с учётом и

получим

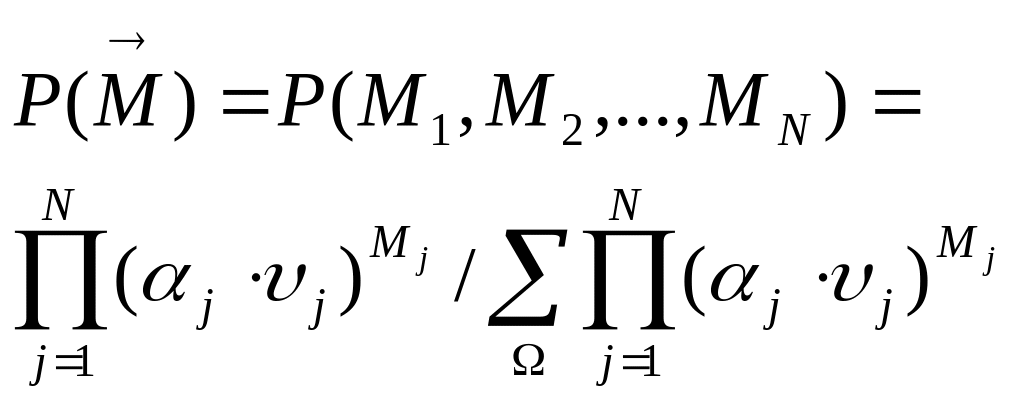
87. Моделирование узловых характеристик объекта на основе разомкнутых сетей мо.

Произв. в след. последовательности:

--- опред. коэф. загрузок СМО

, а также общую загруженность многоканаль-ных СМО ;

--- определяют коэф. , вероятности простоя СМО и вероятности их состояний ;

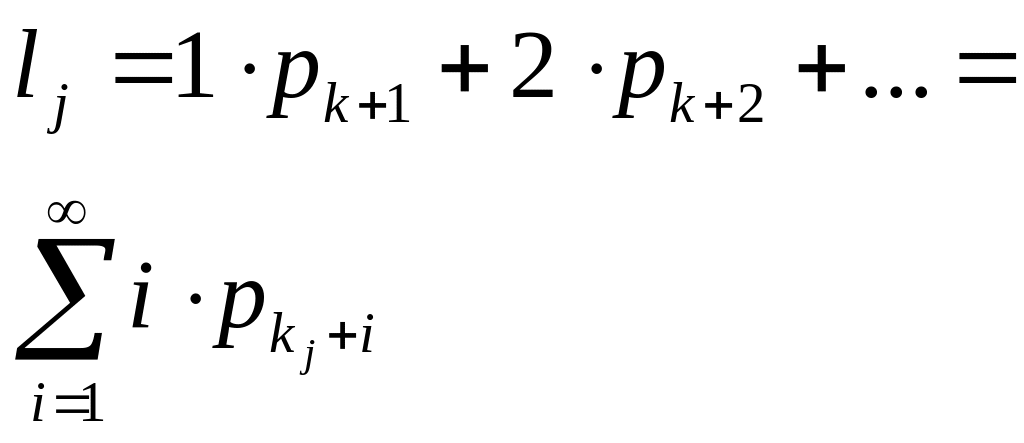--- опред. средние длины очередей к каждой СМО сети по формуле либо для одноканальных СМО как

--- среднее число заявок , находящихся в каждой СМО по формуле , либо для одноканальных СМО как , где общая загруженность рассчитыв. как

--- опред., используя закон Литтла, средн. времена ожидания в очереди и пребывания в СМО по формулам и

88. Моделирование системных характеристик объекта на основе замкнутых сетей мо.

Произв. на базе узловых опред. коэфф. загрузок отдельных СМО ( например, для одноканальных СМО 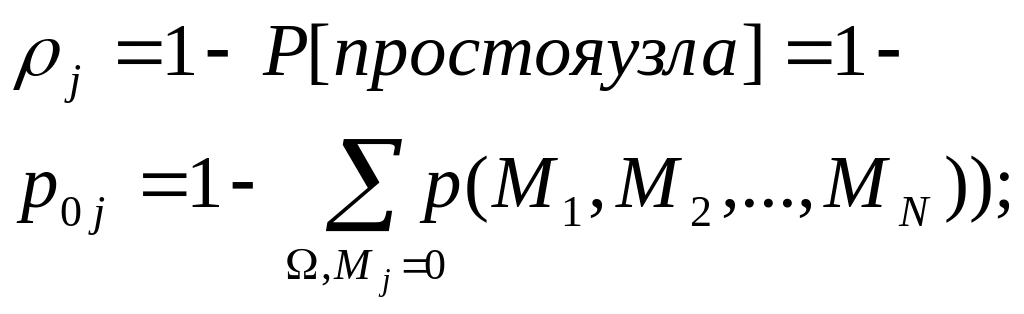--- используя выражения для расчёта коэфф. загрузки, определяют интенсивности потоков заявок в каждую СМО

--- определяют среднюю длину очередей в сети , средн. число заявок в сети и ср. число

обслуживаемых заявок (понятно, что M₀ = L + R);

--- определяют среднее время ожидания в сети , среднее время пребывания заявки в сети и среднее время обслуживания заявки ( понятно, что U = W + T). Значения U и W могут быть определены, учитывая закон Литтла из соотношений и