33.Моделир-е случайных событий, групп событий.

Одно событие:

Событие-факт,кот может происходить или не происходить. Надо смоделир наступление события во времени.

Введ в рассмотрение нов событие Выч-им вер-ть Z:

-случ вел-на,р-константа

Xи Z-равносильн случайные величины

Алгоритм:

1)генерир

2)сравниваем с р

3)если да,то событие Z и Х произошло

Группа событий:

-независ события

События образуют полн группу событий. Они попарно не совместны. В люб момент вр может произойти только одно событие.

Также будем генерир-ть базов послед-ть ,распределён в диапазоне (0;1) равномерно. Можем рассм n событий.

Напр,i –ое событие состоит в том, что Wi попало в i –ый отрезок,т.е

Z и Х-равносильн события. Алгоритм:

1)генерир Wi

2)определ, в какой отрезок попало Wi

3)№ отрезка и есть № произошед-го события

4)повтор процедуру нужное кол-во раз

34.Моделирование зависимых и независ событий.

-произвол события,т.е. потенциально зависимые.

только 4 события(в случае независ событий)

Если знать вер-ти каждого Y,то задача сводится к

-зависимые

Заданы безуслов вер-ти и усл-я вер-ть

-аналогично

Отдельно имитируют ,а затем .

35. Моделирование дискретных случайных величин

Могут задаваться ф-ией плотности(гистограммой) либо ф-ей распределения. Если вел-на явл дискретной, то использ график (табличные значения) ф-ции распред. При этом непрер вел-на сводится к дискрет­ной.

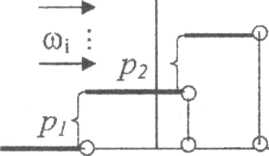
показана ф-ция распре­д дискретной случ вел-ны (

= 1). Так, знач вел-ны Х- x₁x₂,...,x_n можно поставить в соотв вероятн р ,р ,...,р , рассчит по зн-ниям ф-ции распр-ния как

Pk =F_x(xk)-F_x(Xk-1). Указанные зн-ния X образ полн группу событий X = х1, ...,Х= хn, а задача генерации сводится к задаче моделир по­лн группы независ элементарных событий и графич озна­чает "набрасывание" случ числа Wi, на отрезок ед длины по оси О- Y.

36.Моделирование непрерывных случайных величин.

Пусть требуется имитир зн-ия случ в-ны X, для кот задан з-н распред, на­пр, в виде ф-ии распред F_x(x) = Р{Х < х). Если вел-на непре­рывная и ф-ия распр-ия задана аналит, в виде ф-лы, то мо­жно применить метод обратной ф-ции , позвол через ее знач w определить зн-ие аргумента, т.е. F_x{x)=w x=F (w). Если будет получено аналит выр-ие обр ф-ии, то алгоритм гене­рации сост в след: генерир зн-ние Wi, и рассчит очередное зн-ние Xi по фор-ле xi= F (Wi). Напр, для равноме рас­предел величин из ф-ции распред по ф-ле (х - a)/(b - а)=w получают выр-ние =>хi=wi (b-a)+ а для аналитич расчета зн-ий xi

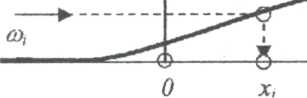
37.Метод обратных функций.

Если известна ф-ия распр-ния, то

P[a<X<b]=Fx (b)-Fx (a). Отсюда можно перейти к дискр. ф-ии распределения

Рассм дискр ф-ию. Вероятности отрезка прямо пропорц длине отрезка. Кажд. отрезок pi задает вер-сть попадания вел-ны в опр интервал. Зная , что представляет кажд отрезок, внутри его можем выбрать 1 зн-ие. Задача сводится к генерации одного события из группы n независ. Событий. Это метод обратных ф-ий , т к мы задаем зн-ие ф-ии и по нему нах зн-ие аргумента

F_x{x)=w x=F (w).