9Поиск решения (Оптимизация)

В состав Excel входит мощное инструментальное средство – Поиск решения. С помощью этого средства можно решать задачи нелинейного программирования, может быть получено решение функционального уравнения, системы линейных уравнений, найден максимум или минимум функции нескольких переменных.

Задачи, которые могут быть решены с помощью инструмента Поиск решения, в общей постановке формулируются так:

Найти значения переменных x₁, x₂, …, x_n, такие, что целевая функция f(x₁, x₂, … , x_n) примет заданное значение, или минимальное значение, или максимальное значение. При этом могут быть заданы ограничения вида g(x₁, x₂, … , x_n), принимающие заданные значения, или значения <= заданных, или значения >= заданных.

Решение оптимизационных задач необходимо начинать с построения математической модели, которая включает:

1. переменные x₁, x₂, … , x_n;

2. целевую функцию f(x₁, x₂, … , x_n);

3. систему ограничений, которым должны удовлетворять переменные.

Искомые переменные – ячейки рабочего листа Excel называются изменяемыми ячейками. На изменяемые ячейки можно наложить дополнительные ограничения, например положительности или целочисленности значений.

1. Лакокрасочное предприятие выпускает краску в двух видах тары – больших и малых банках (барабанах), емкость которых соответственно составляла 55 и 15 л, а стоимость пустых барабанов – 30 и 24 тыс. руб. Литр краски стоит 14600 руб. Некий оптовый покупатель желает приобрести краску на 14 млн. руб. Необходимо, не выходя за пределы договорной суммы, получить от лакокрасочного предприятия, как можно больше краски. При этом имеется возможность лишь указать количество больших и малых барабанов с краской, но нельзя взять краску в разлив.

Решение задачи начнем с построения математической модели:

1. необходимо определить, сколько приобрести больших и малых барабанов с краской. Поэтому переменными являются x₁ – количество больших барабанов с краской, x₂ – количество малых барабанов с краской;

2. необходимо получить, как можно больше краски. Поэтому целевой функцией является f(x₁, x₂) = 55*х₁ + 15*х₂

3. о граничения: (55*14 600 + 30 000)*х₁ + (15*14 600 + 24 000)*х₂ ≤ 14 000 000; х₁, х₂ ≥ 0 х₁, х₂ – целые.

Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.

С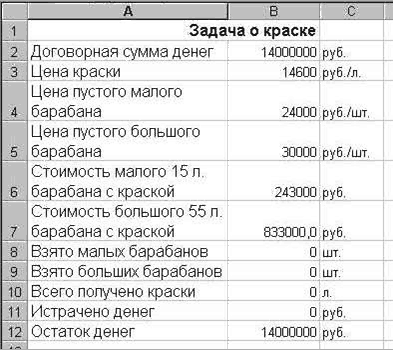 оздайте таблицу, соответствующую(Рисунок 6). При этом в ячейки B4:B7 и B10:B12 запишите очевидные расчетные формулы.

Рисунок 6 Подготовка таблицы Excel для автоматизации выполнения расчетов

Для решения этой задачи применим Поиск решений. В электронной таблице ячейки В8 и B9 будут играть роль изменяемых ячеек, а ячейка B10 – это ячейка с целевой функцией, а В11 – ячейка расчета ограничений.

Проверьте наличие в меню Сервис команды Поиск решения. Если такой команды в этом пункте нет, то ее требуется установить. Для этого выполните команду Сервис, Надстройки, в появившемся окне Надстройки в списке надстроек установите флажок напротив строки Поиск решения.

Выделите ячейку B10 с целевой функцией и выполните команду меню Сервис, Поиск решения. Появится окно Поиск решения (Рисунок 7), в поле Установить целевую которого уже должна быть абсолютная ссылка на ячейку B10.

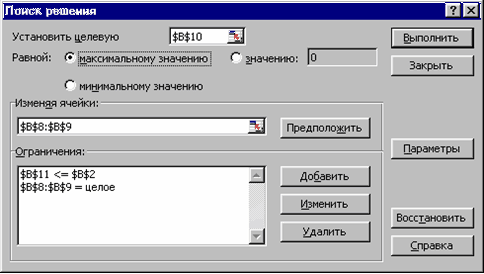
Рисунок 7. Окно Поиск решения

По умолчанию поиск экстремума целевой функции выполняется с допустимой погрешностью 5% (обычная инженерная погрешность). Эта погрешность для рассматриваемого примера слишком велика, так как соответствует 910·0,05=45,5 л краски, что намного больше емкости малого барабана. Погрешность поиска максимума в рассматриваемом примере не должна быть больше емкости малого барабана, которая составляет 15/910·100=1,65 % общего объема краски.

Для повышения требуемой точности поиска решения щелкните на кнопке Параметры окна Поиск решения.

В появившемся окне Параметры поиска решения (Рисунок 8) в поле Допустимое отклонение замените значение на 1,5.

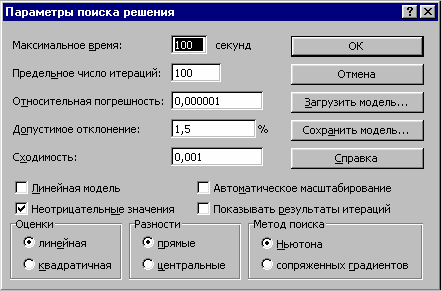
Рисунок 8. Настройка параметров поиска решения

Установите в этом же окне флажок Неотрицательные значения, указав тем самым, что искомые количества барабанов краски не могут принимать отрицательные значения.

Чтобы начать поиск решения, щелкните на кнопке Выполнить окна Поиск решения. После окончания процесса поиска появится окно Результаты поиска.

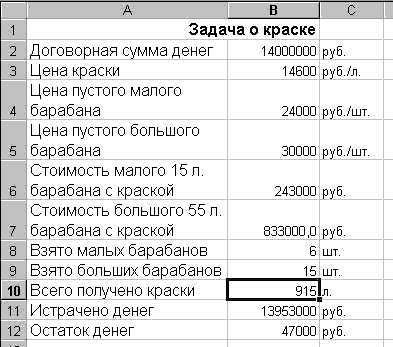
Рисунок 9 Результат поиска максимума объема полученной краски

Итак, наибольшее количество краски будет получено, если взять 15 больших и 6 малых барабанов с краской. И при этом у заказчика будет оставлено 47000 руб.

1. Возможно, более важным является минимизация остатка денег, а не получение максимального количества краски. Решите задачу минимизации остатка денег, (ответ: 11000 руб., если взять 6 больших и 37 малых барабанов).