1. Этапы решения задачи на ЭВМ.

Программирование (programming) - теоретическая и практическая деятельность, связанная с созданием программ. Решение задач на компьютере включает в себя следующие основные этапы, часть из которых осуществляется без участия компьютера.

1. Постановка задачи:

•   сбор информации о задаче;

•   формулировка условия задачи;

•   определение конечных целей решения задачи;

•   определение формы выдачи результатов;

•   описание данных (их типов, диапазонов величин, структуры и т. п.).

2. Анализ и исследование задачи, модели:

•   анализ существующих аналогов;

•   анализ технических и программных средств;

•   разработка математической модели;

•   разработка структур данных.

3. Разработка алгоритма:

•   выбор метода проектирования алгоритма;

•    выбор формы записи алгоритма (блок-схемы, псевдокод и др.);

•    выбор тестов и метода тестирования;

•    проектирование алгоритма.

4. Программирование:

•   выбор языка программирования;

•   уточнение способов организации данных;

•   запись алгоритма на выбранном языке

программирования.

5. Тестирование и отладка:

•   синтаксическая отладка;

•   отладка семантики и логической структуры;

•    тестовые расчеты и анализ результатов тестирования;

•   совершенствование программы.

6. Анализ результатов решения задачи и уточнение в случае необходимости математической модели с повторным выполнением этапов 2-5.

7. Сопровождение программы:

•   доработка программы для решения конкретных задач;

•   составление документации к решенной задаче, к математической модели, к алгоритму, к программе, к набору тестов, к использованию.

2. Оператор выбора. Назначение и правила записи. Примеры.

Простой и составной операторы

Оператор в программе – это единое и неделимое предложение, выполняющее какое-либо действие. Типичный простой оператор – это оператор присваивания. Другим примером может служить вызов какой-либо процедуры в программе. Важно, что под любым оператором подразумевается действие (присваивание, вызов подпрограммы и т.п.). Блоки описания переменных, констант, типов и меток не являются в этом смысле операторами.

Два последовательных оператора обязательно должны разделяться точкой с запятой “;”.

Примеры простых операторов:

a := 10; b := a*5; Write( a, b );

Если какое-то действие мыслится как единое, но реализуется несколькими различными операторами, то последние могут быть представлены как составной оператор.

Составной оператор – это последовательность операторов, перед которой стоит слово BEGIN, а после – END. Слова BEGIN и END часто именую операторными скобками.

Пример составного оператора:

        BEGIN           a := 10;           b :+ a*5;           Write( a, b )         END;

Составной оператор может содержать любое количество простых операторов. Он допускает вложенность, т.е. может содержать внутри себя другие составные операторы.

ВАЖНО: Составной оператор применяется в тех случаях, когда синтаксис языка Паскаль допускает использование только одного оператора, в то время как алгоритм требует задания некоторой последовательности действий. В Паскале все управляющие структуры (операторы) не различают простой и составной оператор: там где стоит простой оператор, можно поставить и составной.

Условный оператор IF

Условный оператор IF служит для организации процесса вычислений (изменения последовательности выполнения операторов) в зависимости от какого-либо логического условия.

Синтаксис оператора IF:

IF Условие THEN Оператор1 ELSE Оператор2;

или

IF Условие THEN Оператор;

Условие может быть представлено логической константой (FALSE – ложь, TRUE - истина), переменной логического типа (Boolean) или логическим выражением.

Если условие истинно, то выполняется оператор (простой или составной), следующий за словом THEN, в противном случае, когда условие ложно, будет выполняться оператор, следующий за словом ELSE. Альтернативная ветвь ELSE может отсутствовать, если в ней нет необходимости. В таком “усеченном” варианте, в случае, если условие оказывается ложным, ничего не происходит и выполняется оператор следующий за условным оператором IF.

Пример 1.

Пусть необходимо составить программу, вычисляющую значение функции:

VAR    x, y : real; BEGIN   Write(‘Введите значение аргумента: ’); ReadLn(x);   IF x>0 THEN y := x           ELSE y := 0;   Write(‘Значение функции y = ’, y) END.

Условные операторы могут быть вложенными друг в друга:

IF Условие THEN if ПодУсловие then ... else ...                   ELSE ...;

Обратите внимание на отсутствие точки с запятой между ключевыми словами.

При вложениях условных операторов самое главное – не запутаться в вариантах сочетаний условий (отчасти этому может помочь ступенчатая форма записи операторов). Всегда действует правило: альтернатива ELSE считается принадлежащей ближайшему условному оператору IF, не имеющему ветви ELSE. Например:

IF Условие1 THEN if Условие2 then Оператор_А             ELSE Оператор_Б;

По записи может сложиться впечатление, что Оператор_Б будет выполняться только при “невыполнении” Условия1. Но на самом деле он будет отнесен к Условию2 и выполнится только при выполнении Условия1 и невыполнении Условия2! Если необходимо, чтобы Оператор_Б выполнялся именно при невыполнении Условия1, то единственный выход таков: заключить вложенный (усеченный) оператор IF в операторные скобки begin…end:

IF Условие1 THEN begin                    if Условие2 then Оператор_А                  end             ELSE Оператор_Б;

В условии оператора IF может стоять достаточно сложное логическое выражение. О правилах построения логических выражений см. раздел “Логические выражения”.

Оператор варианта CASE

Оператор варианта необходим в тех случаях, когда в зависимости от значения какой-либо переменной нужно выполнить те или иные операторы (простые или составные). Если вариантов всего два, то можно обойтись и оператором IF. Но если их, например, десять? В этом случае оптимален оператор варианта CASE.

Синтаксис оператора CASE:

CASE УправляющаяПеременнаяИлиВыражение OF     НаборЗначений1 : Оператор1;     НаборЗначений2 : Оператор2;     НаборЗначений3 : Оператор3;             . . .     НаборЗначенийN : ОператорN     ELSE АльтернативныйОператор END;

Между служебными словами CASE и OF должна стоять переменная или выражение (оно вычисляется при исполнении оператора CASE) целочисленного или любого порядкового типа. Набор значений – это конкретные значения управляющей переменной или выражения, при которых необходимо выполнить соответствующий оператор, игнорируя остальные варианты. Если в наборе несколько значений, то они разделяются между собой запятой.. Можно указывать диапазоны значений, например, 0..9 – все значения от нуля до девяти. Наборы значений и диапазоны можно комбинировать. Между набором значений и соответствующим ему оператором обязательно ставится символ “:”. Значения в каждом наборе должны быть уникальными, т.е. они могут появиться только в одном варианте. Пересечение наборов значений для разных вариантов является ошибкой, и она будет замечена компилятором.

Оператор (Оператор1, Оператор2, …) в конкретном варианте может быть как простым, так и составным.

Пример 1.

PROGRAM Example_CASE_1; VAR A : integer; BEGIN     Write(‘Введите оценку: ‘); Read(A);     CASE A OF         2 : Write(‘неудовлетворительно’);         3 : Write(‘удовлетворительно’);         4 : Write(‘хорошо’);         5 : Write(‘отлично’)         ELSE Write(‘Ошибка!’)     END; END.

Здесь в зависимости от значения переменной А на экран выводится наименование оценки. Наличие варианта ELSE обеспечивает вывод сообщения об ошибке в случае, когда введено число вне интервала 2..5.

Пример 2.

PROGRAM Example_CASE_2; VAR Hour : integer; BEGIN     Read( Hour );     CASE Hour OF         0, 24 : Write(‘Полночь’);         1..4 : Write(‘Ночь’);         5..7 : Write(‘Раннее утро’);         8..11 : Write(‘Утро’);         12 : Write(‘Полдень’);         13..17 : Write(‘День’);         18..23 : Write(‘Вечер’)         ELSE Write(‘Введено число вне диапазона 0..24!’)     END; END.

Оператор цикла с предусловием WHILE

Применяется для организации циклов с неизвестным заранее числом повторений, логика которых предполагает выполнение цикла пока истинно некоторое условие.

Синтаксис оператора WHILE:

WHILE Условие DO Оператор;

Конструкция WHILE…DO переводится как “пока…делать”. Оператор (простой или составной), стоящий после служебного слова DO и называемый телом цикла, будет выполнятся циклически, пока значение “Условия” равно TRUE (истина). Само условие цикла может быть логической константой, переменной или логическим выражением.

Условие выполнения тела цикла WHILE проверяется до начала каждой итерации. Поэтому если условие сразу не выполняется, то тело цикла игнорируется и будет выполнятся оператор, стоящий сразу за телом цикла.

Оператором в теле цикла может быть другой циклический оператор, т.е. циклы могут быть вложенными.

При написании циклов с предусловием следует помнить о двух вещах. Во-первых, чтобы цикл имел шанс когда-нибудь завершится, содержимое его тела должно обязательно влиять на условие цикла. Во-вторых, условие должно состоять из корректных выражений и значений, определенных еще до первого выполнения тела цикла.

Пример цикла WHILE: Вычисление факториала 10! = 1·2·3·4·5·6·7·8·9·10

VAR   Factorial, N : Integer; BEGIN   Factorial := 1; {стартовое значение факториала =0! }   N := 1;         {стартовое значение для условия цикла }   WHILE N<=10 DO                {заголовок цикла, условие }    begin                        {начало тела цикла }      Factorial := Factorial*N; {вычисление факториала N! }      N := N + 1                 {N должно меняться в цикле}    end;                         {конец тела цикла }   WriteLn(’10!= ’,Factorial);  {вывод результата расчета } END.

Обратите внимание на присваивание N:=1 пред циклом. Без него значение N может быть любым, и условие может оказаться некорректным, не говоря уже о самом значении факториала. Значение N меняется внутри цикла. При этом гораздо безопаснее так писать тело цикла, чтобы оператор, влияющий на условие, был бы последним. Это гарантирует от нежелательных переборов. Если, скажем, в рассмотренном выше примере, поставить строку N:=N+1; перед вычислением факториала, то результатом программы будет значение 11!. Исправить оплошность можно, заменив стартовое значение N на 0, а условие – на N<10. Но от этого программа вряд ли станет нагляднее.

Оператор цикла с постусловием REPEAT…UNTIL

Применяется для организации циклов с неизвестным заранее числом повторений, логика которых предполагает выполнение цикла до тех пор пока не станет истинным некоторое условие.

Синтаксис оператора REPEAT…UNTIL:

REPEAT   Оператор1;   Оператор2;   ···    ОператорN; UNTIL Условие;

Операторы (Оператор1, Оператор2, … ОператорN), образующие тело цикла, будут выполнятся циклически, до тех пор пока значение “Условия” не станет равно TRUE (истина). Иными словами, в цикле REPEAT…UNTIL условием продолжения итераций является невыполнение “Условия” (его значение FASLE – ложь).

Условие цикла может быть логической константой, переменной или логическим выражением.

Оператор REPEAT…UNTIL имеет две части: начальную (слово REPEAT) и завершающую (слово UNTIL), которые охватывают группу операторов, составляющих тело цикла. Поэтому необходимости в использовании составного оператора для построения тела цикла из нескольких простых операторов не возникает.

Принципиальное отличие оператора REPEAT…UNTIL от оператора WHILE в том, что проверка условия производится не перед началом выполнения тела цикла, а после его выполнения, когда решается вопрос, повторить ли еще раз действия. Поэтому тело цикла всегда выполняется по крайней мере один раз.

Пример 1. Проверка ввода

VAR   N : Integer; BEGIN   . . .   REPEAT     Write(‘Введите целое число от 0 до 10: ’);     ReadLn(N);   UNTIL (N>=0) and (N<=10);   . . . END.

В этом примере программа будет запрашивать ввод числа до тех пор, пока пользователь не введет “правильное” число.

Пример 2. “Вечный цикл”

REPEAT UNTIL False;

Этот цикл пустой и никогда не прекращающийся. Он хорош только в том случае, когда нужно заблокировать программу, и, возможно весь компьютер. (Но если отбросить шутки, то можно и его пристроить в дело. Обычно так организуют программы с повторяющимися действиями: вначале программы ставят REPEAT, а в конце – UNTIL False. А прервать цикл можно специальными операторами EXIT и HALT). Это имеет смысл, если условий завершения программы много или они очень сложны.)

Оператор цикла с параметром FOR

Оператор цикла с параметром вводится для организации “строгих” циклов, которые должны быть проделаны заданное число раз. Кроме того, циклы с параметром позволяют организовать автоматическое изменение значения некоторой переменной в определенном диапазоне.

Синтаксис оператора FOR:

FOR ПараметрЦикла := МладшееЗначение TO СтаршееЗначение DO Оператор;

или

FOR ПараметрЦикла := СтаршееЗначение DOWNTO МладшееЗначение DO Оператор;

Оператор, представляющий собой тело цикла, может быть как простым, так и составным. Параметр цикла, а также диапазон его значений (от стартового до конечного включительно) может быть только  порядкового (целочисленного. символьного, логического) или перечислимого типа! Параметр цикла это обычная переменная, описанная в текущем блоке. Шаг изменения значения параметра цикла всегда постоянный (в случае целочисленного типа равен единице).

Изменение параметра цикла может быть как возрастающим, так и убывающим. В первом случае МладшееЗначение должно быть больше чем Старшее, а во втором – наоборот.

Примеры оформления циклов с параметром.

VAR i : integer; BEGIN   FOR i := 1 TO 10 DO Write(i:5);   FOR i := 5 DOWNTO 0 DO Write(i:5) END.

На месте младших и старших значений могут стоять константы, а могут и переменные или выражения, совместимые по присваиванию с параметром цикла. Например,

CONST n = 10;       m = 3; VAR i,      k : integer; BEGIN   k := 1;   FOR i := k TO n DO Write(i:5);   FOR i := (m+2) DOWNTO 0 DO Write(i:5) END.

Выполнение цикла начинается с присваивания параметру стартового значения. Затем следует проверка, не превосходит ли параметр конечное значение (случай с TO) или не является ли он меньше конечного значения (случай с DOWNTO). Если результат проверки утвердительный, то цикл считается завершенным. В противном случае выполняется тело цикла (оператор, следующий за словом DO), и после этого параметр цикла меняет свое значение на следующее. Далее снова производится проверка значения параметра цикла, т.е. алгоритм повторяется.

Запрещается изменять параметр цикла и его старшее и младшее значения внутри тела цикла. Кроме того, параметр цикла не может участвовать в построении диапазонов этого же цикла. Компилятор таких “незаконных” действий не замечает, но программа, содержащая цикл с заголовком типа

FOR i := i-5 TO i+5 DO ... ;

не заслуживает никакого доверия, даже если запускается!

Операторы FOR могут быть вложенными друг в друга, например

VAR    i,j : integer; BEGIN   WriteLn(‘Таблица умножения’);   FOR i := 1 TO 10 DO begin      FOR j := 1 TO 10 DO Write((i*j):5);     WriteLn;   end;  END.

Процедуры BREAK, CONTINUE, EXIT и HALT

Процедура BREAK применяется для досрочного прекращения циклов WHILE, REPEAT…UNTIL и FOR.

Пример: Определение номера первого нулевого элемента в массиве А

VAR   i, num : Integer;   A : array[1..10] of Integer; BEGIN   . . . { Ввод элементов массива А }   num := 0;   FOR i:=1 TO 10 DO { Цикл для i от 1 до 10 }    IF A[i]=0 THEN begin { если найден нулевой элемент }                     num := i; { запоминаем его номер }                     BREAK      { прекращаем цикл }                   end;   IF num <> 0 THEN WriteLn(num)               ELSE WriteLn(‘Нулевых элементов нет’); END.

Процедура CONTINUE вызывает переход к следующей циклической итерации игнорируя расположенные ниже операторы, составляющие тело цикла.

Пример: Определение наибольшего общего делителя (НОД) двух чисел

VAR   CommDiv,        { кандидат в НОД }   num1,           { первое число }   num2 : Integer; { второе число } BEGIN   Write(‘Введите первое число: ’); ReadLn(num1);   Write(‘Введите второе число: ’); ReadLn(num2);   FOR CommDiv := num1 DOWNTO 1 DO begin     IF (num2 mod CommDiv)<> 0 THEN CONTINUE;     IF (num1 mod CommDiv) = 0 THEN begin        WriteLn(‘Наибольший общий делитель: ’, CommDiv);        BREAK     end {if} end {for} END.

В примере применен цикл FOR, в котором по убывающий перебираются возможные кандидаты в наибольший общий делитель. Критерий делимости – равенство нулю остатка от деления (операция mod). Если кандидат (значение переменной CoomDiv) не является делителем числа num2, по команде CONTINUE начинается следующий проход цикла, а операторы, оставшиеся в теле цикла, не выполняются. Если число (CommDiv) оказывается делителем числа num2 и num1, что проверяется вторым оператором IF тела цикла, значит, оно – общий делитель. А поскольку перебор идет от больших к меньшим значениям, первый найденный общий делитель – наибольший. Выводим его на печать и прерываем цикл командой BREAK.

EXIT

Процедура EXIT завершает работу своего программного блока. Если EXIT вызывается внутри процедуры или функции, то их работа завершается. Если EXIT вызывается в основном блоке программы, то это приводит к ее завершению.

HALT

Процедура HALT, или более полно HALT(n),   завершает работу программы с кодом завершения n. Этот код впоследствии может быть проанализирован, в частности командой IF ERRORLEVEL в среде MS-DOS. Значение ERRORLEVEL после остановки программы будет равно значению n. Вызов процедуры HALT без параметра эквивалентен вызову HALT(0).

На основе процедуры HALT можно легко построить программу, например ASK.PAS, для организации диалога в BAT-файлах MS-DOS.

Например:

PROGRAM ASK; VAR i : Word; BEGIN   ReadLn(i);   HALT(i) END.

После компиляции получаем файл – AKS.EXE

Пример BAT-файла:

@ECHO OFF CLS ECHO Сейчас вы можете: ECHO 0 - Завершить работу ECHO 1 – Запустить Norton Commander ECHO 2 – Отформатировать жесткий диск ECHO Ваш выбор ? ask.exe IF ERRORLEVEL 0 GOTO end IF ERRORLEVEL 1 GOTO startNC IF ERRORLEVEL 2 GOTO formatHDD GOTO end :startNC    c:\nc\nc :formatHDD    format C: /s :end

3. Понятие алгоритма. Свойства алгоритмов.

Алгоритм - точное предписание исполнителю совеpшить определенную последовательность действий для достижения поставленной цели за конечное число шагов.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге "Об индийском счете" он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных.

Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, - процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.

Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата».

Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.

Такими свойствами являются:

• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.

• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

На основании этих свойств иногда дается определение алгоритма, например: “Алгоритм – это последовательность математических, логических или вместе взятых операций, отличающихся детерменированностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов”.

Такая трактовка понятия “алгоритм” является неполной и неточной.

Во-первых, неверно связывать алгоритм с решением какой-либо задачи. Алгоритм вообще может не решать никакой задачи.

Во-вторых, понятие “массовость” относится не к алгоритмам как к таковым, а к математическим методам в целом. Решение поставленных практикой задач математическими методами основано на абстрагировании – мы выделяем ряд существенных признаков, характерных для некоторого круга явлений, и строим на основании этих признаков математическую модель, отбрасывая несущественные признаки каждого конкретного явления. В этом смысле любая математическая модель обладает свойством массовости. Если в рамках построенной модели мы решаем задачу и решение представляем в виде алгоритма, то решение будет “массовым” благодаря природе математических методов, а не благодаря “массовости” алгоритма.

Виды алгоритмов

Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:

• Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.);

• Гибкие алгоритмы, например стохастические, т.е. вероятностные и эвристические. Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.

• Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.

• Эвристический алгоритм (от греческого слова “эврика”) – это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.

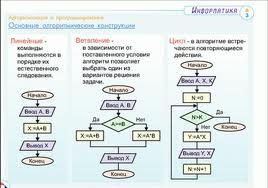
• Линейный алгоритм – набор команд (указаний), выполняемых последовательно во времени друг за другом.

• Разветвляющийся алгоритм – алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.

• Циклический алгоритм – алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов.

Цикл программы – последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторого условия.

Вспомогательный (подчиненный) алгоритм (процедура) – алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.

На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.

Структурная (блок-, граф-) схема алгоритма – графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков – графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия.

Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.

Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации “. Здесь форма представления алгоритма смешивается с самим алгоритмом.

Требования, предъявляемые к алгоритму

Первое правило – при построении алгоритма прежде всего необходимо задать множество объектов, с которыми будет работать алгоритм. Формализованное (закодированное) представление этих объектов носит название данных. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные. Это правило позволяет сразу отделить алгоритмы от “методов” и “способов”. Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.

Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма. Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной. В теории алгоритмов размеры памяти не ограничиваются, т. е. считается, что мы можем предоставить алгоритму любой необходимый для работы объем памяти. В школьной “теории алгоритмов” эти два правила не рассматриваются. В то же время практическая работа с алгоритмами (программирование) начинается именно с реализации этих правил.

В языках программирования распределение памяти осуществляется декларативными операторами (операторами описания переменных). В языке Бейсик не все переменные описываются, обычно описываются только массивы. Но все равно при запуске программы транслятор языка анализирует все идентификаторы в тексте программы и отводит память под соответствующие переменные.

Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно.

Четвертое правило – детерменированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки. Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.

4. Оператор цикла с параметром. Назначение, правила записи. Примеры.

Цикл с параметром

Оператор цикла применяется при выполнении расчетов или других действий, повторяющихся определенное количество раз. Оператор имеет вид:

For i:= N1 To N2 Do "оператор";

либо

For i:= N1 DownTo N2 Do "оператор";

Здесь i - параметр цикла (переменная порядкового типа),

N1, N2 - начальное и конечное значения параметра цикла i.

N1, N2 могут быть константами, переменными или выражениями порядкового типа.

Напомним, что "оператор" может иметь вид: Begin "операторы" end;

Схема выполнения оператора цикла с параметром имеет вид:

В случае связки "To" цикл выполняется при условии N1 <= N2 и происходит с единичным возрастанием параметра цикла i от N1 до N2. В случае связки DownTo цикл выполняется при условии N1 >= N2 и происходит с единичным уменьшением параметра цикла i от N1 до N2.

В операторе цикла не разрешается присваивать параметру цикла какое-либо значение.

После окончания цикла значение параметра цикла "i" неопределенно.

Оператор цикла часто применяется для суммирования значений некоторой последовательности чисел или значений функции при известном числе операций суммирования. Напомним некоторые определения, связанные с расчетом суммы последовательности.

Сумма членов последовательности величин

a₁, a₂, a₃, . . . , a_n

называется конечной суммой

S_n = a₁ + a₂ + a₃+ . . . + a_n

Для некоторых последовательностей известны формулы расчета конечных сумм, например:

при an = an-1 + d; Sn = (a1 + an)*n/2; - арифметическая прогрессия,

при an = an-1 * q; Sn= (a1 - an*q)/(1-q); - геометрическая прогрессия,

где d и q - постоянные числа.

Здесь N-ый член последовательности выражается через (N-1)-ый член. Такие зависимости называются реккурентными.

Конечная сумма последовательности может быть неизвестна, тогда для ее расчета применяется алгоритм суммирования членов последовательности в цикле от 1 до N. Приведем пример расчета конечной суммы последовательности: 12 + 32 + 52 +. . . + (2*N-1)2; Sn = N*(4*N₂-1)/3;

PROGRAM SUM_K; { расчет конечной суммы }

var

a, S, Sn, i, N : word;

Begin

write('Введите число членов суммы N=');

readln(N);

S:= 0;

For i:= 1 to N do

begin { цикл суммирования }

a := Sqr(2*i-1);

S:= S+a

end;

Sn := N*(4*N*N-1) div 3;

Writeln('Конечная сумма S=', S:10:2);

Writeln('Расчет конечной суммы по формуле Sn=', Sn:10:2);

Writeln('Нажми Enter');

ReadLn

End.

В некоторых случаях "N"-ый член последовательности определяется через сумму предыдущих членов, например,

a_n= p*S_n-1,

тогда

S_n= S_n-1 + a_n = S_n-1*(1+р),

и конечную сумму можно рассчитать по формуле:

S_n = S₀*(1+p)N,

где "S₀" - начальная сумма.

Рассмотрим программу вычисления конечной суммы денежного вклада в банк через N месяцев при ежемесячной процентной ставке "pr" (5% cоответствует pr=5).

PROGRAM VKLAD; { расчет конечной суммы вклада в банк }

var

S, Sn, pr : Real;

i, N : Integer;

Begin

Write('Введите начальную сумму вклада S=');

readln(S);

Write('Введите процент по вкладу pr=');

readln(pr);

Write('Введите количество месяцев вклада N=');

readln(N);

For i:= 1 to N do S:= S*(1+pr/100); { цикл произведений }

Writeln('Конечная сумма вклада S=', S:10:2);

{ Оператор для расчета "Sn" напишите самостоятельно }

Writeln('Расчет конечной суммы вклада по формуле Sn=', Sn:10:2);

Writeln('Нажмите Enter');

readln

End.

Часто применяются вложенные операторы цикла. Например, если необходимо провести все варианты расчета при изменении нескольких параметров в заданных диапазонах.

Составим программу расчета функции y = A*sin(x) - cos(x)/A; при изменении аргумента "x" в диапазоне от 0 до Pi с шагом Pi/100 и при изменении параметра "A" в диапазоне от 1 до 3 с шагом 0.5.

Program tabl;

var

y, x, a, dx : real;

i, j: integer;

Begin

Writeln(' Расчет по формуле: y=A*sin(x)-cos(x)/A; ');

Writeln('--------------------------------------------------');

Writeln('| X | A=1.0 | A=1.5 | A=2.0 | A=2.5 | A=3.0 |');

Writeln('--------------------------------------------------');

dx := pi/100;

for i:= 0 to 100 do

begin { внешний цикл изменения аргумента "X" }

x:= dx*i;

Write( x:8:4 );

for j := 1 to 5 do

begin{ вложеннный цикл изменения параметра "A" }

A := 0.5*(j+1);

y := A*sin(x)-cos(x)/A; Write(y:8:4)

end;

Writeln; {перевод курсора на новую строчку}

if ((i+1) mod 20) = 0 then readln{задержка прокрутки экрана до нажатия Enter}

end;

readln;

End.