1. Вычисление статистических характеристик выборки.

1.Найдите выборочные характеристики для и , в скобках указаны имена необходимых функций, аргументом этих функций является диапазон значений:

- наибольшее значение (МАКС),

- наименьшее значение (МИН),

- объем выборки (СЧЕТ)

- выборочную среднюю по определению (проверьте с помощью СРЗНАЧ),

- медиану: значение, которое делит вариационный ряд на две равные (по числу значений) части (МЕДИАНА),

- вариационный размах: разница между наибольшим и наименьшим значениями выборки,

- выборочную дисперсию по определению (проверьте с помощью ДИСПР),

- выборочное среднее квадратическое отклонение по определению (проверьте с помощью СТАНДОТКЛОНП),

2. Эти же значения определите с помощью стандартных средств Excel — надстройки Сервис/Анализ данных/Описательная статистика, не забудьте отметить поле Итоговая статистика и разместите результаты расчета на том же листе.

2. Построение доверительных интервалов.

Для значений доверительной вероятности и вычислите доверительные интервалы для генеральной средней используя найденные в предыдущем пункте значения выборочных характеристик по формуле

,

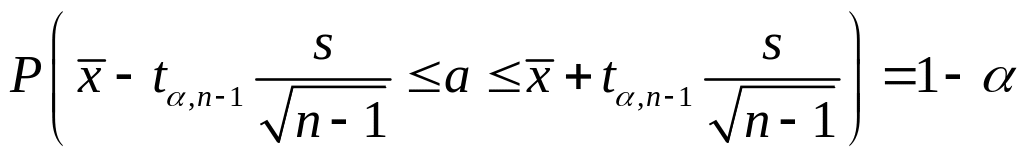Здесь — выборочное среднее квадратическое отклонение.

Значения найдите по таблице распределения Стьюдента как критическую точку двусторонней области, соответствующую доверительной вероятности и степени свободы (см. приложение) и проверьте с помощью функции СТЬЮДРАСПОБР, аргументами которой являются:

Вероятность – значение

Степени_свободы - количество степеней свободы, равное .

3. Проверка статистических гипотез

1. Для уровней значимости и проверьте гипотезу о том, что значение генеральной средней для выборки значений равно 100

Для этого:

1. Вычислите выборочное значение статистического критерия

, где — исправленное среднее квадратическое отклонение (СТАНДОТКЛОН).

2. По таблице Стьюдента по заданному уровню значимости и числу степеней свободы найдите критическую точку (для двусторонней области). Проверьте найденное значение с помощью функции СТЬЮДРАСПОБР.

3. Если , то нет оснований отвергнуть нулевую гипотезу.

Если , то нулевая гипотеза отвергается в пользу альтернативной.

3. Для указанных уровней значимости проверьте гипотезу о статистической значимости выборочной средней, т.е. гипотезу

4. Проверка гипотезы о равенстве дисперсий нормальных генеральных совокупностей

1. Рассматривая значения и как выборки из нормальных генеральных совокупностей проверьте гипотезу о равенстве их генеральных дисперсий:

.

Для этого:

1. Вычислите выборочное значение -статистики

,

где — исправленные выборочные дисперсии.

2. По таблице критических точек распределения Фишера-Снедекора с помощью функции FРАСПОБР найдите критическую точку , соответствующую уровню значимости и степеням свободы и .

3. Сделайте вывод о существенности различия дисперсий:

• Если , то нулевая гипотеза отвергается,

• Если , то нет оснований отвергнуть нулевую гипотезу.