Билет 1

1) Предмет и задачи метрологии.

Метрология — наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Метрологию разделяют на:

• Теоретическая метрология занимается вопросами фундаментальных исследований, созданием системы единиц измерений, физических постоянных, разработкой новых методов измерения.

• Прикладная (практическая) метрология занимается вопросами практического применения в различных сферах деятельности результатов теоретических исследований в рамках метрологии.

• Законодательная метрология включает совокупность взаимообусловленных правил и норм, направленных на обеспечение единства измерений, которые возводятся в ранг правовых положений (уполномоченными на то органами государственной власти), имеют обязательную силу и находятся под контролем государства.

Объектами метрологии являются:

Измерение — нахождение значения величины опытным путем с помощью специальных технических средств.

Погрешность измерения — разность между результатом измерения и истинным значением измеряемой величины.

Средство измерения — техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу величины, размер которой принимается неизменным в пределах установленной погрешности в течение известного интервала времени.

Эталон единицы величины — средство измерений, предназначенное для воспроизведения и хранения единицы величины, кратных или дольных ее значений с целью передачи ее размера другим средствам измерений данной величины.

Единство измерений — состояние измерений, при котором их результаты выражены в узаконенных единицах величин, а погрешности измерений не выходят за установленные границы с заданной вероятностью.

2) Электротехнические измерения и их особенности.

Электроизмерительные приборы различных систем (магнитоэлектрические, электродинамические, электростатические) получают энергию с помощью приведения в действие своего отсчетного устройства непосредственно от объекта измерения (участка электрической цепи), искажая, тем самым, действительное значение измеряемой величины, т.е. потребляют существенную мощность от источника сигнала измерительной информации.

Ограниченный диапазон частот токов и напряжений – от 0 (постоянный ток) до нескольких килогерц. Чаще всего электроизмерительные приборы применяются для измерений в электросетях промышленной частоты (50,60,400 Гц), особенно в трехфазных.

Типовые средства измерений в электроизмерениях:

вольтметры, амперметры, ваттметры, счетчики электрической энергии, меры ЭДС.

Диапазоны измеряемых величин:

Напряжение – от десятков микровольт до сотен киловольт

Мощность – от долей ватта до сотен киловатт

Частота – от постоянного тока (0 Гц) до десятков килогерц (исключение составляют термоэлектрические приборы(диапазон частот токов и напряжений до 30 МГц) и электростатические киловольтметры (до 100 МГц))

3) Произвести статистическую обработку массива результатов наблюдений.

Билет 2

1) Проверка нормальности распределения результатов наблюдений.

При помощи χ2 – распределения

Е сли имеем n независимых измерений величины Х, распределенной нормально, то сумма:

распределена как χ2 с числом степеней свободы f = n – 1 (0 ≤ χ2 < ∞).

значения χ2 в зависимости от вероятности P(χ2 > χ2q) = q и числа степеней свободы (f) табулированы в виде процентных точек распределения в таблицах математической статистики: χ2q( f ) = «положительное число».

Проверка гипотезы о нормальном распределении СВ при помощи χ2 –критерия (критерий Пирсона)

Имеем выборку объемом n измерений:

1 шаг – упорядочение выборки: х₁ ≤ х₂ ≤ х₃ ≤ … ≤ х_n

2 шаг – разбиение интервала ( х₁ , х_n ) на произвольное число интервалов ( t_k ) и подсчет наблюдений (частот – ν_i ) , попавших в каждый интервал.

3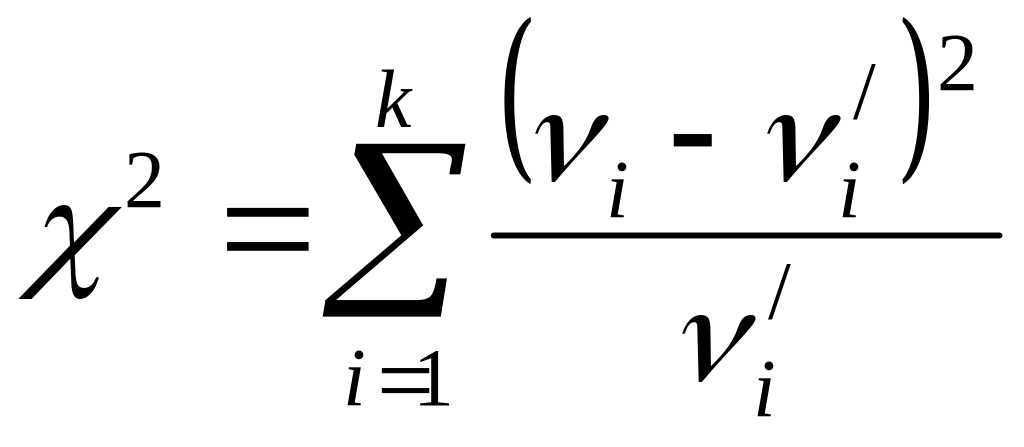 шаг – определение с помощью теоретического распределения числа теоретических частот (ν^١_i = n·P_i) в интервале.

Сумма

распределена как χ2 с числом степеней свободы

f = k - 1 - l , где: k - число интервалов; l - число связей, накладываемых на выборку при оценке параметров распределения, для вычисления теоретических частот.

Формулировка основной и альтернативной гипотез

Н₀: наблюдаемые отклонения от нормального распределения носят случайный характер.

Н₁: отклонения от нормального закона не случайны.

И спользуется односторонний критерий!

Условие принятия основной гипотезы:

Ограничения, накладываемые на критерий Пирсона

• Критерий является приближенным, поэтому k ≥ 5 .

• Группы (разряды) где ν^١ < 5 объединяют с соседними.

• Объем выборки должен быть достаточно велик: n ≥ 50.