2.5. Частные случаи расположения плоскостей в пространстве

Рассмотрим изображение на комплексном чертеже и свойства плоскостей частного положения: плоскости, перпендикулярные и параллельные плоскостям проекции.

Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости.

1. Горизонтально проецирующая плоскость ₁.

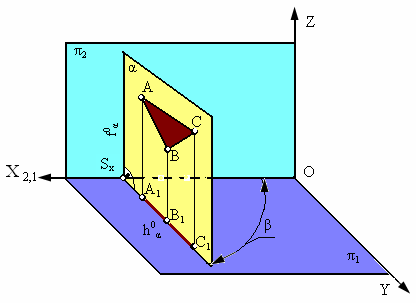
Рис. 2.13. Изображение горизонтально-проецирующей плоскости

Плоскость , перпендикулярная горизонтальной плоскости проекции ₁, называется горизонтально проецирующей (рис. 2.13).

Основным свойством горизонтально проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на ₁ в прямую линию (горизонтальный след плоскости h_0).

Угол , который составляет горизонтальный след плоскости h_0 c координатной осью Х, равен углу наклона плоскости  к плоскости проекций ₂. Фронтальный след такой плоскости перпендикулярен оси Х (f_0  X).

2. Фронтально проецирующая плоскость   ₂. Плоскость  перпендикулярная фронтальной плоскости проекций ₂ называется фронтально проецирующей (рис. 2.14).

Рис. 2.14. Изображение фронтально-проецирующей плоскости

Основным свойством фронтально-проецирующей плоскости является то, что любая фигура. Расположенная в этой плоскости, проецируется на ₂ в прямую линию (фронтальный след плоскости f_0). Угол , который составляет фронтальный след плоскости f_0 с координатной осью Х, равен углу наклона плоскости  к плоскости проекций ₁. Горизонтальный след такой плоскости перпендикулярен оси Х.

Плоскости, параллельные плоскостям проекций

(плоскости уровня)

1. Горизонтальная плоскость ₁.

Плоскость , параллельная плоскости ₁, называется горизонтальной (рис. 2.15).

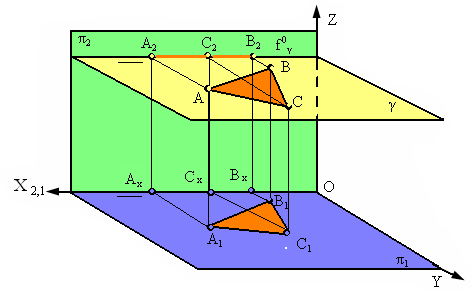
Рис. 2.15. Изображение плоскости, параллельной горизонтальной плоскости проекций

Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскости проекций в натуральную величину ( А₁В₁С₁=АВС, рис. 17). Фронтальный след этой плоскости параллелен оси Х (f_0Х).

2. Фронтальная плоскость ₂.

Плоскость , параллельная плоскости ₂, называется фронтальной.

Любая фигура расположенная в такой плоскости. Проецируется на фронтальную плоскость проекций без искажения, т. е. в натуральную величину.

Горизонтальный след фронтальной плоскости параллелен оси Х.

Примечание. Плоскость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскостей.

Плоскость общего положения

Плоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций – произвольные, но отличные от 0 и 90) называется плоскостью общего положения (рис. 2.16.а).

На комплексном чертеже следы плоскости общего положения составляют с осью проекций также произвольные углы.