5 Формула шеннона.

Количество информации для равновероятных и неравновероятных событий; формула Шеннона; объёмный (алфавитный) подход к измерению информации.

Вероятность некоторого исхода события выражается в долях единицы и равна отношению количества повторений данного исхода события к общему числу повторений события: р=K/N, где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого-то процесса. Чтобы определить, какова вероятность получения каждой оценки в задаче №3, нужно подсчитать общее количество разных оценок, полученных за контрольную работу. Определив, какую часть от общего числа оценок составляют двойки, найдем вероятность получения двойки. Затем, определив, какую часть от общего количества составляют тройки, найдем вероятность получения тройки. Доля четвёрок среди всех оценок – это вероятность получения четверки, а доля пятёрок - это вероятность получения пятёрки.

Зная вероятности событий, можно определить количество информации в сообщении о каждом из них. Согласно теории информации, для этого нужно решить показательное уравнение 2ⁱ=1/Р, т.е. I=log₂1/Р = - log₂P где I – это количество информации в сообщении о неравновероятностном событии, P – вероятность события Ответить на этот вопрос нам поможет формула вычисления количества информации для Можно ли применить формулу К. Шеннона для равновероятных событий? Если p1=p2=..=pn=1/N, тогда формула принимает вид: или Мы видим, что формула Хартли является частным случаем формулы Шеннона.

6Системы счисления. Представление чисел в различных позиционных системах счисления

Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда)

Представление числа

Целое число без знака в -ричной системе счисления представляется в виде конечной линейной комбинации степеней числа ^[1]:

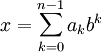, где  — это целые числа, называемые цифрами, удовлетворяющие неравенству

Каждый базисный элемент в таком представлении называется разрядом (позицией), старшинство разрядов и соответствующих им цифр определяется номером разряда

Запись числа

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число записывают в виде последовательности его -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо^[1]:

В ненулевых числах левые нули обычно опускаются. Во избежание путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса:

Построение такой записи числа называют позиционным кодированием числа, а саму запись — позиционным кодом числа. Количество записываемых кодов такой записью определяется в комбинаторике и равно количеству размещений с повторениями:

, где

— размерность множества из которого берутся цифры ( основание системы кодирования), — количество цифр в записи. При и показательной весовой функции , при этом образуются системы счисления с равномерным распределением чисел на числовой оси c расстояниями между соседними числами на числовой оси равными . Из-за этих двух свойств такие системы счисления получили наибольшее распространение.

С помощью позиций в -ричной системе счисления с можно записать целые числа в диапазоне от до ( ), то есть всего различных чисел с расстояниями между соседними числами на числовой оси равными .

Запись чисел

Для записи чисел в системах счисления с основанием до 36 включительно в качестве цифр (знаков) используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и, затем, буквы латинского алфавита (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z). При этом, a = 10, b = 11 и т. д., иногда x = 10.

При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:

 — это число 123 в десятичной системе счисления;

 — то же число в восьмеричной системе счисления;

 — то же число, но в двоичной системе счисления;

 — то же число, но в десятичной системе счисления с двоичным кодированием десятичных цифр (BCD);

 — то же число, но в несимметричной троичной системе счисления;

 — то же число, но в симметричной троичной системе счисления, знаки "i", "7", "2" и "-" обозначают "-1", знаки "1" и "+" обозначают "+1".

В некоторых специальных областях применяются особые правила указания основания.

В русских счётах для записи чисел в десятичной показательной позиционной системе счисления применяется унарнодесятичная система записи (представления) десятичных цифр с одной избыточной унарнодесятичной цифрой «1111111111»= на каждый