Параметрические и непараметрические модели оу. Расчет динамических свойств оу статистическими методами.

Идентификация объекта, в общих словах, это построение математической модели объекта для его теоретического исследования либо для применения в качестве эталона процесса в реальной САУ. Математические модели, равно как и виды индетификации, бывают: параметрическими, непараметрическими, рекуррентными.

Параметрические модели связаны с четким аналитическим построением зависимостей выходных сигналов ОУ от сигналов, подводимых на его входы.

Динамические характеристики (переходная характеристика, частотная переходная функция и др.) характеризуют протекание временных процессов в ОУ и по их виду можно судить о времени протекания переходного процесса и других показателях качества. Во многих случаях ОУ можно рассматривать как систему динамических звеньев или (в вырожденном случае) как динамическое звено. Зная динамические характеристики динамических звеньев, входящих в ОУ, можно получить динамические характеристики самого ОУ.

Поведение ОУ в динамике часто описывается нелинейными ДУ.

В ТАУ применяют несколко способов составления уравнений динамики ОУ. Первый способ – когда дифференциальные или разностные уравнения составляются аналитически на основе анализа физических процессов, которые могут происходить в ОУ; второй – с помощью экспериментально определенных статических характеристик, представленных в виде графиков; третий – по данным таблиц, полученных также экспериментальным путем, с последующей их обработкой методами регрессионного анализа; четвертый способ – основан на использовании аналогового или цифрового моделирования.

При использовании статических характеристик для составления уравнений ОУ применяется метод линеаризации, сущность которого заключается в замене нелинейной составляющей линейной в некотором диапазоне изменения переменных. Такая замена в случае достаточно гладких нелинейностей практически возможна во всем рабочем диапазоне изменения переменных.

Реализация процедур и методов оценки параметров моделей оу.

На практике часто применяется интегральная оценка параметров ОУ.

На ОУ в процессе его функционирования действуют возмущения, различные по величине и физической природе. Для учета лидирующих возмущений возможно применение принципа регулирования по возмущению.

В соответствии с этим принципом в зависимости от величины возмущения УВМ может вносить коррекцию в математическую модель процесса, сокращая тем самым методическую ошибку системы. Учет всех возмущений, действующих на ОУ данным методом невозможен из-за бесконечного количества каналов данных возмущений. Поэтому на практике рекомендуется интегральная оценка физического процесса совместно с возмущениями и помехами в КС исходя из теоремы Котельникова. Теорема гласит, что любая функция времени S(t), обладающая ограниченным спектром W может быть представлена в виде бесконечной суммы, члены которой представляют собой произведение:

.

Величины представляют значения исходной функции времени S(t), определенной в дискретные моменты времени K/2W. Эти величины называются отсчетами или отсчетными значениями функции S(t). Дробный множитель:

называется функцией отсчетов. При функция отсчетов принимает вид (см. рис.1).

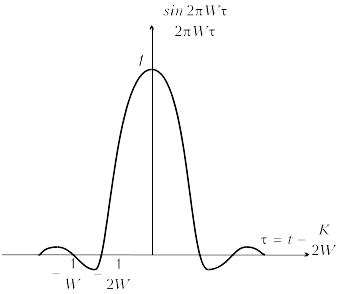
Рис.1

Основные свойства функции отсчетов:

1. В момент времени t=k/2W функция отсчетов достигает max=1.

2. В момент времени функция отсчетов обращается в нуль.

1. Ширина главного лепестка функции отсчетов на нулевом уровне равна:

.

Отсюда следует, что min длительность импульса, который может существовать на выходе селективной системы с полосой W, равна 1/W.

4. Функции отсчетов ортогональны на бесконечно большом интервале времени.