
Понятие производной : Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как пределотношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Геометрический и физический смысл производной : Основная статья: Касательная прямая
Если
функция ![]() имеет
конечную производную в точке
имеет
конечную производную в точке ![]() то
в окрестности
то
в окрестности ![]() её
можно приблизить линейной
функцией
её
можно приблизить линейной
функцией
![]()
Функция ![]() называется
касательной к
называется
касательной к ![]() в
точке
в
точке ![]() Число
Число ![]() является
угловым коэффициентом
или тангенсом угла наклона касательной
прямой.
является
угловым коэффициентом
или тангенсом угла наклона касательной
прямой.
[Править]Скорость изменения функции
Пусть ![]() —
закон прямолинейного движения.
Тогда
—
закон прямолинейного движения.
Тогда ![]() выражает мгновенную
скорость движения
в момент времени
выражает мгновенную
скорость движения
в момент времени ![]() Вторая
производная
Вторая
производная ![]() выражает мгновенное
ускорение в
момент времени
выражает мгновенное
ускорение в
момент времени
Вообще
производная функции ![]() в
точке
в
точке ![]() выражает
скорость изменения функции в точке
,
то есть скорость протекания процесса,
описанного зависимостью
выражает
скорость изменения функции в точке
,
то есть скорость протекания процесса,
описанного зависимостью ![]()
Производная сложной ф-ии : Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке , а функция g имеет производную в точке
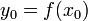 ,
то сложная функция h(x) = g(f(x)) также имеет
производную в точке
.
,
то сложная функция h(x) = g(f(x)) также имеет
производную в точке
.
Дифференциал
высших ф-ии : Дифференциал
функции ![]() в
точке
в
точке ![]() может
быть определён как линейная функция
может
быть определён как линейная функция
![]()
где ![]() обозначает производную
в
точке
.
обозначает производную
в
точке
.
Таким
образом ![]() есть
функция двух аргументов
есть
функция двух аргументов ![]() .
.
Дифференциал
может быть определён напрямую, т.е., без
привлечения определения производной
как функция ![]() линейно
зависящая от
линейно
зависящая от ![]() и
для которой верно следующее соотношение
и
для которой верно следующее соотношение
![]()
Производные высших порядков
Если
функция ![]() дифференцируема
при всех
дифференцируема
при всех ![]() ,
то мы можем рассмотреть функцию
,
то мы можем рассмотреть функцию ![]() ,
сопоставляющую каждой точке
,
сопоставляющую каждой точке ![]() значение
производной
значение
производной ![]() .
Эта функция
.
Эта функция ![]() называется
производной функции
называется
производной функции ![]() ,
или первой
производной от
.
(Иногда саму исходную функцию
называют нулевой
производной и
обозначают тогда
,
или первой
производной от
.
(Иногда саму исходную функцию
называют нулевой
производной и
обозначают тогда ![]() .)
Функция
.)
Функция ![]() ,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала
,
в свою очередь, может иметь производную
во всех (или некоторых) точках
интервала ![]() ,
которую мы обозначим
,
которую мы обозначим ![]() и
назовём второй
производной функции
.
Если предположить, что вторая
производная
и
назовём второй
производной функции
.
Если предположить, что вторая
производная ![]() существует
во всех точках
,
то она может также иметь производную
существует
во всех точках
,
то она может также иметь производную ![]() ,
называемую третьей
производной функции
,
и т. д. Вообще,
,
называемую третьей
производной функции
,
и т. д. Вообще, ![]() -й
производной функции
называется
производная от предыдущей,
-й
производной функции
называется
производная от предыдущей, ![]() -й
производной
-й
производной ![]() :
:
![]()
если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.
Дифференциалы
высших порядков :
Дифференциалом порядка n,
где n
> 1 от
функции ![]() в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1),
то есть
в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1),
то есть
![]() .
.
5)
Неопределённый интеграл : Неопределённый
интегра́л для
функции ![]() —
это совокупность всех первообразных данной
функции.
—
это совокупность всех первообразных данной
функции.
Если
функция
определена
и непрерывна на промежутке ![]() и
и ![]() —
её первообразная, то есть
—
её первообразная, то есть ![]() при
при ![]() ,
то
,
то
![]() ,
,
где С — произвольная постоянная.
![]()
![]()
![]()
![]()
Если ![]() ,
то и
,
то и ![]() ,
где
,
где ![]() —
произвольная функция, имеющая непрерывную
производную
—
произвольная функция, имеющая непрерывную
производную
6) Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
7) Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
![]()
для определённого:
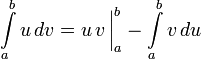
Предполагается,
что нахождение интеграла ![]() проще,
чем
проще,
чем ![]() .
В противном случае применение метода
неоправдано.
.
В противном случае применение метода
неоправдано.
8) Дифф. 1го порядка : Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят явно производные искомых функций до некоторого порядка. Если неизвестными являются функции двух или более переменных, то уравнения называются уравнениями в частных производных. В противном случае, то есть если искомая функция зависит только от одного вещественного независимого переменного, уравнения называются обыкновенными дифференциальными уравнениями. В этом курсе будем иметь дело только с последними.
Так как во многих физических приложениях независимым переменным, от которого зависят неизвестные искомые функции, является время, то в дальнейшем, как правило, независимое переменное будет обозначаться через t. Неизвестные функции будут обозначаться через x, y, z и т.д.
Рассмотрим в первую очередь одно дифференциальное уравнение первого порядка. Общий вид такого уравнения следующий:
|
9) Дифф. 2го порядка : Дифференциальным уравнением называется уравнение, связывающее между собой независимые переменные, их функцию и производные (или дифференциалы) этой функции.
Порядок старшей производной, входящей в данное дифференциальное уравнение, называется порядком этого уравнения.
Таким образом общий вид дифференциального уравнения n-го порядка следующий
![]() ,
,
10) Матрицей размера
m на n (записывается так ![]() )называется
совокупность mn вещественных (комплексных)
чисел или элементов другой структуры
(многочлены, функции и т.д.), записанных
в виде прямоугольной таблицы, которая
состоит из m строк и n столбцов и взятая
в круглые или прямоугольные или в двойные
прямые скобки. При этом сами числа
называются элементами
матрицы и
каждому элементу ставится в соответствие
два числа -номер
строки и номер
столбца.
)называется
совокупность mn вещественных (комплексных)
чисел или элементов другой структуры
(многочлены, функции и т.д.), записанных
в виде прямоугольной таблицы, которая
состоит из m строк и n столбцов и взятая
в круглые или прямоугольные или в двойные
прямые скобки. При этом сами числа
называются элементами
матрицы и
каждому элементу ставится в соответствие
два числа -номер
строки и номер
столбца.
Для
обозначения матрицы используются
прописные латинские буквы, при этом
саму матрицу заключают в круглые или
прямоугольные или в двойные прямые
скобки. Элементы
матрицыобозначают
строчными латинскими буквами, снабженными
двумя индексами: ![]() -
элемент матрицы, расположенный
в i-й строке
и j-м столбце
или коротко элемент в позиции (i,j).
В общем виде матрица размера m на n может
быть записана следующим образом
-
элемент матрицы, расположенный
в i-й строке
и j-м столбце
или коротко элемент в позиции (i,j).
В общем виде матрица размера m на n может
быть записана следующим образом

11) Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
14)
Ко́мпле́ксные[1] чи́сла (устар. Мнимые
числа[2]), —
расширение поля вещественных
чисел,
обычно обозначается ![]() .
Любое комплексное число может быть
представлено как формальная сумма
.
Любое комплексное число может быть
представлено как формальная сумма ![]() ,
где
,
где ![]() и
и ![]() —
вещественные числа,
—
вещественные числа, ![]() — мнимая
единица[3].
— мнимая
единица[3].
Комплексные
числа образуют алгебраически
замкнутое поле —
это означает, что многочлен степени ![]() с
комплексными коэффициентами имеет
ровно
комплексных
корней (основная
теорема алгебры).
Это одна из главных причин широкого
применения комплексных чисел в
математических исследованиях. Кроме
того, применение комплексных чисел
позволяет удобно и компактно сформулировать
многие математические модели, применяемые
в математической физике и в естественных
науках — электротехнике, гидродинамике, картографии, квантовой
механике, теории
колебаний и
многих других.
с
комплексными коэффициентами имеет
ровно
комплексных
корней (основная
теорема алгебры).
Это одна из главных причин широкого
применения комплексных чисел в
математических исследованиях. Кроме
того, применение комплексных чисел
позволяет удобно и компактно сформулировать
многие математические модели, применяемые
в математической физике и в естественных
науках — электротехнике, гидродинамике, картографии, квантовой
механике, теории
колебаний и
многих других.
Алгебраическая
форма : Запись комплексного числа ![]() в
виде
,
в
виде
, ![]() ,
называется алгебраической
формой комплексного
числа.
,
называется алгебраической
формой комплексного
числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что ![]() ):
):
![]()
![]()
