§9. Движение в неинерциальных системах отсчета.

Мы отмечали, что второй закон Ньютона справедлив в инерциальных системах отсчета. Тем не менее, второй закон Ньютона можно использовать и в неинерциальных СО.

Ускоренное движение неинерциальной системы отсчета относительно инерциальной приводит к появлению дополнительных сил, называемых силами инерции. Рассмотрим два случая.

а) Неинерциальная система отсчета движется поступательно относительно инерциальной с постоянным ускорением w₀

Это означает, что штрихованные оси координат сохраняют свое направление в инерциальной системе отсчета.

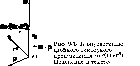
Рис. 9.1. Штрихованная система отсчета движется поступательно относительно не штрихованной с постоянным ускорением w₀. Пояснения в тексте.

Запишем связь линейных кинематических параметров точки М в обеих системах отсчета. По-прежнему будем полагать, что t = t.

Положение точки М в инерциальной СО r связано с ее положением в неинерциальной СО соотношением(см. рис.9.1):

r = r + R_O. (9.1)

Продифференцируем это выражение по времени. Получим:

v = v + v_O. (9.2)

В этом случае приняты следующие названия скоростей.

v = v_абс – скорость точки в инерциальной СО называется абсолютной скоростью.

v = v_отн – скорость точки в СО, движущейся относительно первой, называется относительной скоростью.

v_O = v_пер – скорость движения точки М, связанная с движением неинерциальной СО, называется переносной скоростью. В данном случае это движение, обусловленное поступательным движением неинерциальной СО.

Таким образом имеем: v_абс = v_отн + v_пер .

Дифференцируя выражение (9.2) по времени, получим связь между ускорениями точки М в обеих системах:

w = w + w₀. (9.3)

В этих выражениях w, w и w₀ – ускорения точки М в инерциальной СО, ускорение точки М в неинерциальной СО и ускорение неинерциальной СО, соответственно.

Умножив (9.3) на массу материальной точки М, получим:

mw = mw – mw₀. (9.4)

Это выражение является уравнением движения материальной точки в неинерциальной СО, движущейся поступательно. Правая часть этого уравнения формально представляет собой сумму сил, действующих на материальную точку в неинерциальной СО.

Первое слагаемое mw – это произведение массы т материальной точки на ее ускорение w в инерциальной системе отсчета, которое по второму закону Ньютона равно сумме всех сил взаимодействия, действующих на нее: mw = .

Второе слагаемое (–mw₀) – это произведение массы т материальной точки на ускорение w₀ неинерциальной системы отсчета, движущейся поступательно, взятое с обратным знаком. По размерности эта величина является силой, которая называется поступательной силой инерции F_ин.

F_{ин_} = – mw₀.

Первое слагаемое является суммой «настоящих сил» в том смысле, что они есть результат взаимодействия тел. Поскольку эти силы зависят только от разностей координат и разностей скоростей взаимодействующих точек, эти силы являются инвариантными в нерелятивистском случае при переходе от одной СО к другой.

Сила инерции F_ин не является результатом взаимодействия, а возникает в результате ускоренного движения неинерциальной системы отсчета. При переходе к другой системе отсчета меняются и силы инерции. Очевидно, что они не является инвариантами. И еще одна особенность сил инерции – у нее нет «партнера». К силам инерции в принципе не применим третий закон Ньютона.

Таким образом, в нашем случае ускорение материальной точки в неинерциальной системе отсчета w можно вычислить из уравнения:

w = .(9.5)

б) Силы инерции при ускоренном движении начала отсчета и равномерном вращении системы отсчета

Рассмотрим, к каким силам инерции приводит равномерное вращение осей координат штрихованной СО.

По-прежнему выполняется соотношение (9.1) r = r + R_O (рис.9.1).

В случае б) оси координат штрихованной системы отсчета не сохраняют своего направления в пространстве, как в предыдущем случае. Это необходимо учесть при взятии производной . Запишем r в координатном виде и возьмем от нее производную:

.(9.6)

При выводе этого соотношения мы учли (2.13), что =е_i.

Таким образом,

v = v +   r +v_O. (9.7)

Возьмем производную от абсолютной скорости v (9.7).

;

;

;

.

Таким образом, .

При взятии производной мы учли, что  = const и (9.6).

Двойное векторное произведение rможно легко раскрыть, представив вектор r как сумму векторов r_ и  , где r_ и  – составляющие радиус-вектора вдоль оси вращения и перпендикулярно к ней соответственно (см. рис 9.1). Тогда r = r_ + ´ = ´, т.к. вектора  и r_ параллельны. Используя теперь правило раскрытия двойного векторного произведения (2.12), получим:´´r¢ =  = –².

Окончательно имеем:

w = w +2v – w²r + w_O. (9.8)

Для названий ускорений в этом выражении приняты следующие термины:

w = w _абс – ускорение точки в инерциальной системе отсчета – абсолютное ускорение.

w = w_отн – ускорение этой же точки в неинерциальной системе отсчета – относительное ускорение.

2v = –2v = w_кор – кориолисово ускорение.

w_O– w²r = w_пер – переносное ускорение.

Обратимся теперь к написанию уравнений движения в нашей неинерциальной системе отсчета. Поступим точно так же, как и в предыдущем случае: во второй закон Ньютона (7.1) подставим выражение (9.8) и перенесем все члены в правую часть за исключением члена, содержащего относительное ускорение. Получим:

w = . (9.9)

Таким образом, для написания уравнения движения в неинерциальных системах отсчета необходимо добавить к силам взаимодействия две силы инерции: переносную силу инерции и силу Кориолиса.

Переносная сила инерции в нашем случае состоит из двух слагаемых.

Первое слагаемое (– тw_O¢) знакомо нам по предыдущему случаю и называется поступательной силой инерции. Эта сила возникает из-за ускоренного движения начала О неинерциальной системы отсчета. Эти силы мы постоянно ощущаем, пользуясь городским транспортом.

Второе слагаемое тw²r называется центробежной силой инерции. Центробежные силы вызывают перегрузки у летчиков, исполняющих фигуры высшего пилотажа. Они используются в центробежных сушилках, сепараторах.

Сила Кориолиса т2v, возникает только тогда, когда неинерциальная система отсчета вращается со скоростью , а материальная точка движется относительно этой системы со скоростью v. Поскольку Земля вращается, система отсчета, связанная с ней не является инерциальной, и, следовательно, мы должны ожидать различные проявления сил инерции. Так при строгом рассмотрении движения тел относительно Земли мы должны учитывать центробежные силы инерции, равные т²Rcos, где т – масса тела,  – угловая скорость суточного вращения Земли, R – радиус Земли,  – широта. При расчете движения снарядов на большие расстояния необходимо учитывать влияние на траекторию полета сил Кориолиса. Важным проявлением действия сил Кориолиса является изменение положения плоскости качаний маятника Фуко, что послужило еще одним доказательством суточного вращения Земли.

Еще раз напомним, что все написанные уравнения движения материальных точек применимы только когда скорости движения много меньше скорости света.

Примеры.

Поезд массы т =2000т движется на северной широте  = 60.

а) Определить модуль и направление силы бокового давления поезда на рельсы, если он движется вдоль меридиана со скоростью v = 54км/час;

б) Как должен двигаться поезд, чтобы результирующая сил инерции, действующая в системе отсчета Земля, была равна нулю?

Отв. а) f =mvcos = 3,8кН; б) по параллели с востока на запад со скоростью v = (_зR_з/2)cos  420км/час.