§ 4. Определение потерь давления

Потери давления происходят в результате потерь энергии газового потока на трение Р_тр и местные сопротивления Р_м. _с. Установлено, что Р_тр и Р_м, _с пропорциональны скоростному давлению.

Потери давления на трение

Р

Рис. 15. Истечение газа из отверстия с острыми кромками

тр — ^ (^Мгидр) ЩРо (1 0it)/2, (3)

где X —коэффициент трения; L —длина трубы, м; d_rllJXV —гидрав­лический диаметр канала, м. Для практических расчетов К прини­мают равным для кирпичных каналов 0,05—0,06; для металличе­ских труб 0,02—0,03.

Потери давления на местные сопротивления

, ^M.c = S^OPo(l ~f <*0/2,

где | —коэффициент местного сопротивления, определяемый опыт­ным путем (см. прил. 1).

48

§ 5« Истечение газов через отверстия

Истечение газов через отверстия наблюдается при выби­вании газов через отверстия печи, работе горелок, форсунок и т. д.

Количество газа, истекающего через отверстие, зависит от дав­ления, под которым происходит истечение, площади и формы по­перечного сечения отверстия. Для определения количества газа используем уравнение давлений и запишем его в развернутом и преобразованном виде

я, (р_в - Р,.) g + (р; - Р_в) + wfa/2 =

= Hi (рв — Pr)d + (P_r — Рв) -f- W2p_r/2 4“ рпот = const,

где Н₁ (р_в — р_г) g, Н₂ (р_в — р_г) g — избыточные геометрические давления в сечениях / и II (Р'_Г — Р_в), (Р_г — ^_в) — избыточные статические давления в сечениях 1—1 и II—II (см. рис. 14).

Рассмотрим истечение несжимаемого газа через отверстие при постоянной температуре.

Отверстие с острыми кромками. Представим себе, что из сосуда неограниченно больших размеров (давление газа в котором Р_г) газ вытекает через отверстие сечением F в газовую среду с давлением Р₂. Требуется определить скорость истечения. Напишем уравнение дав­лений для сечения /—I и II—//, показанных на рис. 15. Темпера­тура газа постоянна, поэтому Р

геом — Ргеом •

Потерями на трение в данном случае можно пренебречь. При этом уравнение давлений имеет вид

Pi ^iPir/2 = Рг ^2pfr/2*

Так как сосуд имеет неограниченно большие размеры, то w₁ = 0. Если Р₂ = Pq, то получим

^ = />0 + ^/2.

Обозначим Р_г — Р₂ = Р\ тогда

w₂= V 2Р/р*_г м/с. (4)

Сечение струи газа F₂ будет меньше сечения F благодаря сжатию струи. Отношение FJF называется коэффициентом сужения струи и имеет различные значения в зависи­мости от условий истечения. Для тон­ких стенок сосуда F₂/F—0,63.

Определим расход газа V в сечении 11 = 11:

V₂ = w₂F₂, но F₂ = F₂F!F\ тогда расход газа, м³/с

• = (F.F/F) |/ 2ЯТр^.

Рис. 16. Истечение газа через цилиндрический насадок:

а — с острыми кромками; б — с закругленными кромками

Пример 1. По трубе d = 53 мм протекает воздух, имеющий температуру 0° С (р = 1,29 кг/м³) со скоростью 2 м/с. Коэффициент трения А, = 0,04. Длина трубы 10 м. Определим потери давления по формуле (3):

Ртр = 0,04 (10/0,053) 2²-1,29 (1 + (1/273)-0)/2 - 19,5 Па. ¹

Пример 2. Определить скорость истечения газа из отверстия с острыми кром­ками, если давление газа перед отверстием Р_г = 110 кПа; давление среды, в которую истекает газ, Р₀ = 105 кПа; плотность газа р/_г =1,15 кг/м³; температура газа 0 °С. Перепад давлений

р ==• Pi— р₂ = ПО 000 — 105 000 = 5000 Па.

Скорость истечения по формуле (4)

w = /2-5000/1 Лб == 93,5 м/с.

Отверстие с цилиндрическим насадком. Форма насадка и вход­ных кромок при прочих равных условиях значительно влияет на количество истекающего газа. Рассмотрим случай истечения газа через цилиндрический насадок с острыми кромками (рис. 16, а).

Уравнение давлений для сечений /—/ и Ill-Ill имеет вид

Р\ = Р₃ + ^зр*_г/2 + (w₂ — w₃)² p_tr/2,

где wlp_tr/2 — скоростное давление в сечении III—III; (w₂—

• ^з)²Р^г/2 потери давления на сжатие струи.

Из уравнения сплошности следует

w₂F₂ = w₃F_3i

откуда w₂ = w₃F₃iF₂.

Подставив последнее выражение в уравнение давлений и пре­образовав его, получим

Pi~P3^(wl/2){\+[(F₃/FJ-m_Ptr.

Принимаем F₂/F₃ = 0,63, заменяем Р_± — Р₃ = Р> получаем рас­ход газа, м³/с

V = 0,85^ У^/ри-

При истечении газа через цилиндрический насадок с закруглен­ными кромками потерь на сужение струи нет (рис. 16, б).

Уравнение давлений для сечений /—/ и II—II в этом случае имеет вид

P_{1 =} P_{2 + W}I_PU/ 2. -

Заменяя Р_г — Р₂ = Р, получим расход газа, м³/с

' v = F₂VWIftr-

При истечении газа через диффузор (расширяющийся насадок) с закругленными кромками на входе (рис. 17) уравнение давлений для сечений /—I и II—II имеет вид

Pi = Pi -f ^iptr/2.

Подставляя "P_A — P₂ — P, получим расход газа, м³/с

• = F₂i 2Pj^_v.

Из сравнения рассмотренных случаев видно, что наибольший расход при одном и том же значении Р наблюдается в случае диффу­зора с закругленными кромками на входе, так как при этом FJF = = 1. Диффузор не должен расширяться более чем на 7°, так как это примерно соответствует естественному расширению струи газа. Диффузоры широко применяют в технике (инжекционные горелки, эжекторы для создания искусственной тяги и т. д.).

Выбивание газов через открытые окна печей. При нормальном режиме работы печи на ее поду поддерживается атмосферное давле­ние. По высоте печи это давление возрастает и достигает максимума под сводом. Количество газов (м³/с), выбивающихся через окно (значительных размеров) печи (рис. 18),

V = (2/3) НВ 1/ 2Я (ров - рог)/Р*г»

где Н и В —высота и ширина окна, м.

Рис. 18. Истечение газа через окно печи

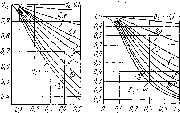
Рис. 30, Графики для расчета нагрева и охлаждения: а — поверхности плиты; б — поверхности цилиндра

где t_ne4 — температура печи, °С; С_в — температура поверхности тела в конце нагрева, °С; /”_ов — температура поверхности тела в на­чале нагрева, °С; /д — температура центра тела в конце нагрева, °С;

• температура центра тела в начале нагрева, °С; а—коэффи­циент теплоотдачи между средой и телом, Вт/(м²-К); S — расчетная толщина тела, м; % — теплопроводность тела, Вт/(м-К); а — коэф­фициент температуропроводности тела, м²/с; т — время нагрева тела, с.

Графическая зависимость 0_ПОВ = cp (Bi, Fo) для плиты и цилиндра показана на рис. 30, а, б. По графикам определяют температуру поверхности тела. Графическая зависимость 0„ = <p (Bi, Fo) для плиты и цилиндра показана на рис. 31, а, б. По графикам можно определить температуру центра тела. Пример расчета нагрева тела приведен в § 3 гл. XIII.

■а) 6)

Рис. 31. Графики для расчета нагрева и охлаждения: а — середины плиты; б — середины цилиндра