6.2. Общие сведения из теории свободных волн на поверхности воды
Теоретическое описание волнения основано на решении уравнений Навье–Стокса и неразрывности в предположении о безвихревом, или потенциальном, характере движения, т. е. в предположении
В таком случае можно ввести понятие потенциала скорости φ такого, что:
При этих предположениях уравнение неразрывности (5.3.2) принимает форму уравнения Лапласа:
В качестве граничных условий принимают условие непротекания жидкости через дно:
где z = -H — глубина моря, а также кинематическое граничное условие, определяющее связь между отклонением свободной поверхности от положения равновесия
и вертикальной составляющей скорости на свободной поверхности, т. е. при z = ξ:
В случае очень глубокого моря (H >> λ) решение уравнения (6.2.3) с граничным условием (6.2.5) описывает так называемые «волны бесконечно малой амплитуды», профили которых имеют вид:
Таким образом, такая волна является синусоидальной с амплитудой у поверхности a = Cω/g. Здесь k = 2π/λ — волновое число, ω = 2 π/τ — круговая частота, C — постоянная интегрирования.
Гребни и подошвы волны (6.2.6) находятся в точках, для которых kx – ωt = πn/2, где n. = 0, ±1, ±2, ..., или x = ωt/k + πn/2k, откуда видно, что координаты этих точек меняются во времени, и, следовательно, волна перемещается со скоростью с = ω/k. В гидродинамике доказывается, что ω2 = kg. Тогда для фазовой скорости получим
Аналогично
Траекториями движения частиц в волне являются окружности. На поверхности (z = 0) радиус окружности равен амплитуде волны (r0 = а), а с глубиной радиусы убывают по закону:
На глубине z1 = λ/2 и z2 = λ эти радиусы составляют соответственно 1/23 и 1/535 от r0.
На конечной глубине профиль волны представляет собой синусоиду:
с амплитудой a = Cω ch(kH)/g (здесь ch(kH) — гиперболический косинус. Напомним, что ch(x) = (exp(x) + ехр(-х))/2 и гиперболический синус sh(x) = (ехр(х) – ехр(-х))/2).
Траектории движения частиц в волне на конечной глубине представляют собой эллипсы с большой горизонтальной и малой вертикальной полуосями, равными соответственно:
На дне при z = H
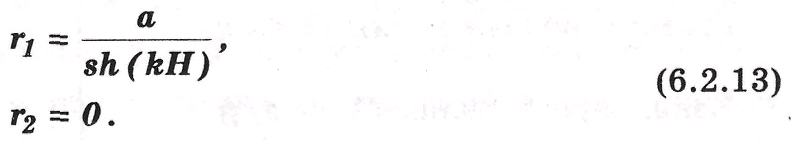
Следующее приближение — трохоидальная волна и т. д.
Впервые теория поверхностных волн была развита в трудах Стокса. Он обнаружил, что кроме периодического отклонения частиц в волне от исходного положения имеется еще и постоянное смещение частиц в горизонтальном направлении.
Скорость этого движения при бесконечной глубине моря равна
Отсюда видно, что эта скорость очень быстро затухает с глубиной. Так, на глубине z = 0,5λ скорость переносного движения составляет всего лишь ~ 0,2% от переносной скорости на поверхности.
В общем случае в линейном приближении для ровного дна (H = const) потенциал скорости и отклонение уровня свободной поверхности от положения равновесия z = 0, как следует из решения (6.2.3) с граничными условиями (6.2.4), (6.2.5), равны соответственно:
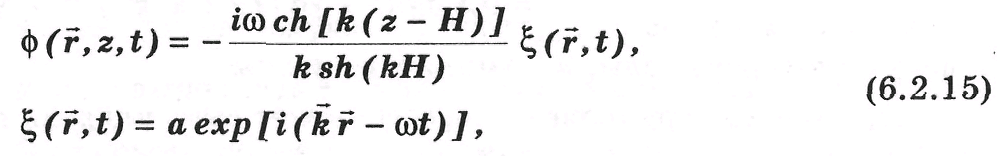
где r = r(x,y).
Волны на поверхности жидкости обладают дисперсией, выражающейся в зависимости их скорости распространения от частоты. Эта зависимость выражается так называемым дисперсионным соотношением:
Частные случаи дисперсионного соотношения (6.2.16) приведены в таблице 6.2.1. (Где γ — коэффициент поверхностного натяжения, отнесенный к плотности воды.)
Волны делят на гравитационные и капиллярные в зависимости от того, какая сила — гравитационная или поверхностного натяжения — для них играет доминирующую роль:
λ < 0,2 см — капиллярные волны;
0,2 см < λ < 20 см — гравитационно-капиллярные волны;
λ > 20 см — гравитационные волны.
Скорость перемещения отдельных гребней, т. е. фазовая скорость, равна:
что для глубокой и мелкой воды соответственно можно переписать в виде:
Энергия волнового движения в линейном приближении может быть записана в виде:
где ρ — плотность воды, a — амплитуда волны.
И, наконец, групповая скорость может быть найдена по формуле:
В частности, для волн на глубокой воде из (6.2.20) следует cg = 0,5 c.