5.3.1. Дрейфовые течения

Представим себе, что над безграничной поверхностью очень глубокого однородного по плотности океана дует длительное время равномерный ветер. Течение, вызванное им, установилось. Однородность ветра по горизонтали, огромные пространства исключают возможность появления наклона уровня океана и возникновения вертикальных составляющих скорости движения воды, а большая глубина исключает влияние дна на характер движения. В этом случае система уравнений (5.3.1) примет вид:

Или, вводя a² = ω sin φ/α µ, где α = 1/ρ — удельный объем, вместо (5.3.3) получим:

Решение системы (5.3.4) при граничных условиях на поверхности:

(что означает, что ветер дует вдоль оси y) имеет вид:

Отсюда видно, что на поверхности вектор скорости течения отклонен вправо от направления ветра на 45° (Северное полушарие) и равен

Из (5.3.6) далее следует, что скорость течения уменьшается с глубиной, а •поток его отклоняется все более и более вправо. На некоторой глубине скорость оказывается направленной в сторону, противоположную вектору скорости на поверхности. Это происходит на глубине z = π/a, определяющейся коэффициентом трения. Ее называют глубиной трения и обозначают буквой D:

На этой глубине величина скорости равна:

т. е. движение практически заключено в поверхностном слое толщиной D, что составляет сотни метров. Этот слой часто называют слоем Экмана.

На глубине z = 2D скорость равна:

Интегрируя (5.3.6) по z от 0 до ∞ легко показать, что для всей толщи моря полный поток воды направлен под углом 90° вправо от ветра в Северном полушарии и равен:

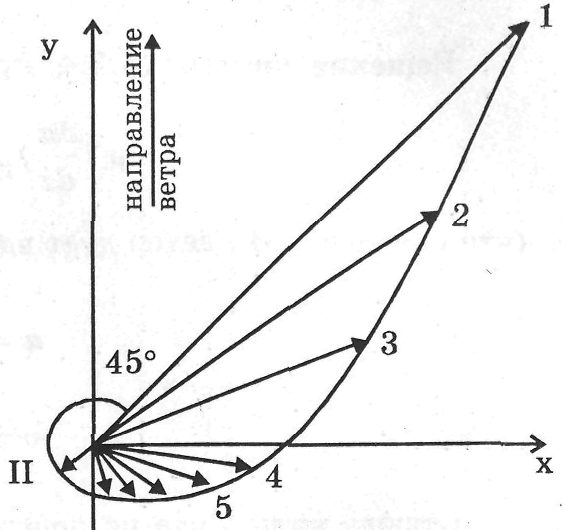
Вернемся к (5.3.6) и изобразим проекцию вектора дрейфового течения на горизонтальную плоскость (рис. 5.3.1).

Рис. 5.3.1. Изменения скорости и направления дрейфового течения с глубиной. Стрелки — проекции скорости течения на горизонтальую плоскость. Точку I соответствует поверхности воды, точка II — глубине D.

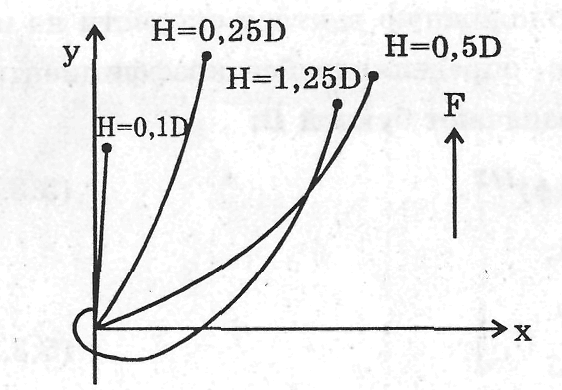Рис. 5.3.2. Изменение скорости и направления дрейфового течения с глубиной при различных отношениях H/D.

Если глубина моря не очень велика, то при решении системы (5.3.4) требуется задать равенство нулю составляющих скорости u и v на дне. Этим учитывается трение воды о дно. Решение показывает, что при этом изменение вектора скорости по глубине будет существенно иным. Его отклонение от направления ветра оказывается меньшим, чем 45°, и зависящим от глубины моря. При очень малых глубинах моря по отношению к D дрейфовый поток практически по всей глубине совпадает с направлением ветра. Однако, если глубина Н хотя бы немного больше D, море практически можно считать «бесконечно глубоким», т. к. при этом распределение векторов скорости дрейфового течения по глубине практически ничем не отличается от их распределения в случае очень глубокого моря.

Природным явлениям, как правило, скачкообразные изменения не свойственны. Поэтому нельзя ожидать, что и отклонение течения под действием силы Кориолиса при переходе через экватор должно изменяться с правого на левое, или наоборот, мгновенно. И действительно, уже попытка учесть влияние дна на величину отклонения дрейфового течения на поверхности в близких к экватору областях подтверждает это. Очевидно, что у экватора влияние дна будет сказываться и при очень больших глубинах.

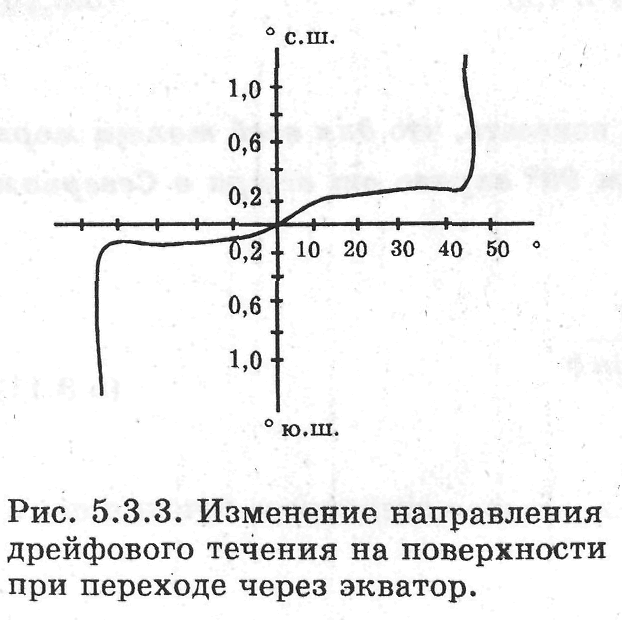
А связано это с тем, что, как показывает формула (5.3.8), глубина трения D зависит и от широты. При подходе к экватору D стремится к бесконечности. На рис. 5.3.3 изображен ход изменения отклонения вектора поверхностной скорости дрейфового течения при переходе через экватор с учетом влияния глубины.