5.2. Силы, действующие на морскую воду
5.2.1. Сила увлечения ветра
При движении воздуха над поверхностью воды между водой и воздухом возникает сила трения, вызывающая движение воды — дрейфовое течение. Эту силу называют тангенциальной силой трения.
Наблюдениями в природе и в лабораторных условиях установлено, что эта сила может быть выражена так:
где c — эмпирическая константа, ρ0 — плотность воздуха, V — скорость ветра на стандартной высоте (2 м над сушей и 10 м над морем соответственно).
Величина тангенциальной силы трения или ее проекции на соответствующие оси координат могут быть также определены по вертикальному градиенту скорости воды у самой поверхности и коэффициенту вязкости, т. е. коэффициенту трения между горизонтальными слоями воды µ:
где ось z направлена вертикально вниз. Именно в таком виде сила трения ветра вводится в уравнение движения как условие на верхней границе.
5.2.2. Сила градиента давления
Мы уже знаем, что течения создают у берегов или в зоне конвергенции и дивергенций подъем или понижение уровня.
В результате вдоль горизонтальных поверхностей, мысленно проведенных на различных глубинах, давление оказывается не одинаковым, возникает горизонтальный градиент давления, а следовательно, и горизонтальная составляющая силы давления. Это учитывается наличием в уравнениях Навье–Стокса соответствующих членов вида
Давление столба воды равно:
где ρ — плотность воды, g — ускорение свободного падения.
Пусть наклон уровня направлен так, как показано на рис. 5.2.1. Тогда
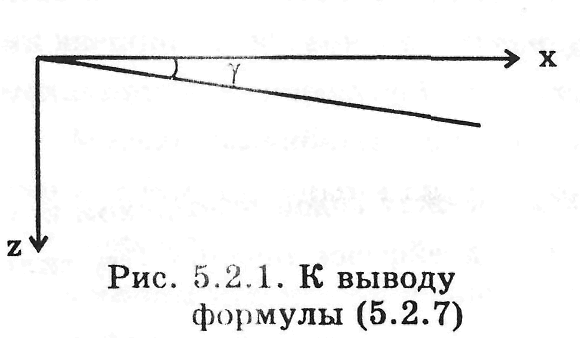
С учетом (5.2.5) получим
Учитывая, что γ — малый угол, вместо (5.2.6) можно написать
В дальнейшем мы используем выражение (5.2.7).
5.2.3. Сила внутреннего трения
Сила внутреннего трения, или сила турбулентного трения, приводящая к диссипации турбулентной энергии, выражается обычно в виде:
где ∂u/∂n — изменение скорости вдоль направления n, а µ' — коэффициент турбулентного трения.
5.2.4. Сила Кориолиса
Сила Кориолиса вызвана вращением Земли вокруг своей оси и выражается следующим образом:
где v — скорость тела относительно поверхности Земли, ω — угловая скорость вращения Земли.
Выберем правостороннюю систему координат XYZ так, чтобы плоскость XY находилась на поверхности Земли, а ось OZ была направлена вниз. Тогда проекции Fк на соответствующие оси будут иметь к вид:
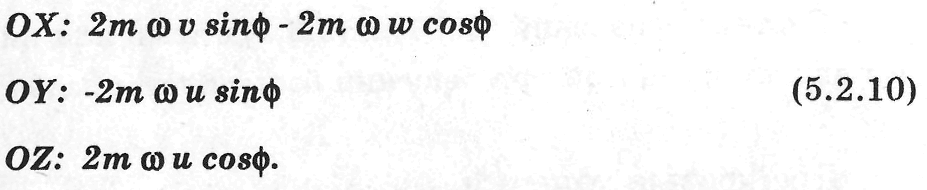
Как правило, вертикальной составляющей скорости течения w пренебрегают, тогда вместо (5.2.10) получим:
где u, v — проекции скорости течения на оси X и Y, φ — широта точки на поверхности Земли.
Направление силы Кориолиса можно определить по правилу левой руки (для Северного полушария). Если расположить левую руку ладонью вниз, а четыре вытянутых пальца направить по скорости течения, то отогнутый большой палец покажет направление силы Кориолиса. Отсюда следует, что под действием силы Кориолиса в Северном полушарии потоки отклоняются вправо от направления течения.
5.3. Дрейфовое течение
Закономерности большой группы движений в океане описываются известной системой уравнений Навье–Стокса:
где u, v, w — проекции скорости течения на оси x, y, z; t — время; p — давление; ρ — плотность; X, Y, Z — проекции внешних сил, действующих на частицы жидкости; µ — коэффициент вязкости. Начало координат расположено на поверхности воды и оси x и y направлены вдоль нее, а ось z — в глубь океана. Уравнение неразрывности имеет вид:
Система уравнений (5.3.1) и (5.3.2) с теми или иными граничными условиями является основой при решении большинства задач динамики океана.