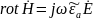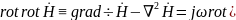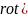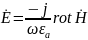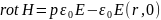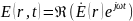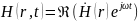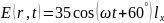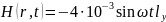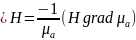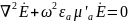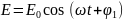Формулы для экзамена по ЭдиРРв.
1 Глава
ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
Для характеристики величины и направления скорости изменения скалярного поля вводят градиент этого поля
Декартова система координат (x,y,z)
;
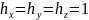Цилиндрическая
система координат (r,
,
z)
;
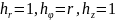Сферическая
система координат (r,
.
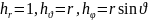Градиент вычисляют
;
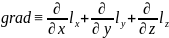В цилиндрической системе координат
;
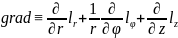В сферической системе координат
.
Дивергенцию векторного поля А вычисляют путем дифференцирования его проекций по правилам:
в декартовой системе координат
;
в цилиндрической системе координат
;
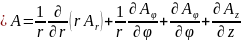в сферической системе координат
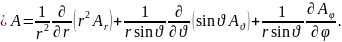
В произвольной ортогональной криволинейной системе координат
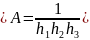
Проекции ротора векторного поля имеют вид:
В декартовой системе координат
В цилиндрической системе координат
;
В сферической системе координат
Ректор векторного поля А в произвольной системе координат выражают через проекции исходного поля и коэффициенты Лямэ:
Дифференциальные операции со скалярными и векторными полями
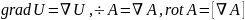
Символический вектор Гамильтона
Оператор
,
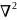закон действия на векторное поле А
Операция, действующая на скалярное поле, задается оператором Лапласа
В декартовой системе координат
В цилиндрической системе координат
В сферической системе координат
.
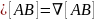
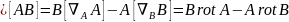
2 Глава. Уравнения максвелла
Для вакуума
Закон сохранения электрического заряда
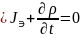
Плотность тока смещения
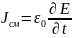
Ток проводимости с объемом плотности
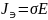
Электрический ток поляризации с объемом
Вектор электрического смещения (индукции)
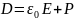
В результате ур-ие Максвелла приобретает вид
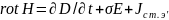
Вектор намагниченности М и вектор магнитной индукции В, связанный с Н и М соотношением
Второе ур-ие Максвелла в материальной среде
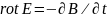
Третье и четвертое ур-ие Максвелла
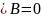
В не слишком сильных полях как поляризованность, так и намагниченность линейно связаны с напряженностями полей
Материальное ур-ия электромагнитного поля
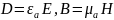
Относительные проницаемости
Материальные ур-ия
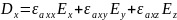
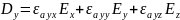
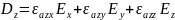
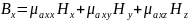
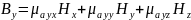
Ур-ия Максвелла в дифференциальной форме
Уравнения Максвелла в интегральной форме
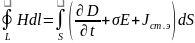
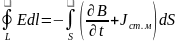
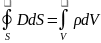
Относительно комплексных амплитуд полей
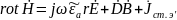
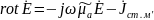
В
эти ур-ия входят комплексные диэлектрическая
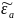и магнитная
проницаемости
Тангенсы углов диэлектрических и магнитных потерь
Нормальные и тангенциальные составляющие
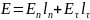
Нормальные составляющие индукций и тангенциальные составляющие напряженностей непрерывны в каждой точке границы раздела
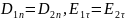
Тангенциальная составляющего электрического вектора отсутствует
Электрический ток с поверхностной плотностью
Объемная плотность энергии в любой точке пространства
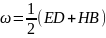
Закон сохранения энергии в теореме Пойнтинга
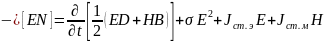
Вектор Пойнтинга
Комплексный вектор Пойнтинга
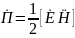
Действительная часть этого вектора
Лемма Лоренца
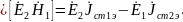
Примеры типовых задач
Волновые уравнения
Система из двух первых ур-ий Масквелла, справедливых для вакуумав отсутствие сторонних источников
Операция rot во втором ур-ии системы
Два первых ур-ия Максвелла относительно комплексных амплитуд
