Свойства функции распределения:

1) 0≤F_ξ(x)≤1

2) F_ξ(x) является неубывающей ф-цией своего аргумента, т.е. если х₁<х₂ → F_ξ(x₁) ≤F_ξ(x₂)

Событие А, состоящее в том, что ξ<x₂

P(ξ<x₂)=P(ξ<x₁)+P(x₁≤ ξ<x₂)

F_ξ(x₂) = F_ξ(x₁) + P(x₁≤ ξ<x₂)

≥0

Следовательно, F_ξ(x₂)≥F_ξ(x₁) ч.т.д.

3) P(x₁≤ξ≤x₂)= F_ξ(x₂) - F_ξ(x₁)

4) Если все возможные значения случайной величины распределены на всей числовой прямой, то справедливы следующие предельные соотношения:

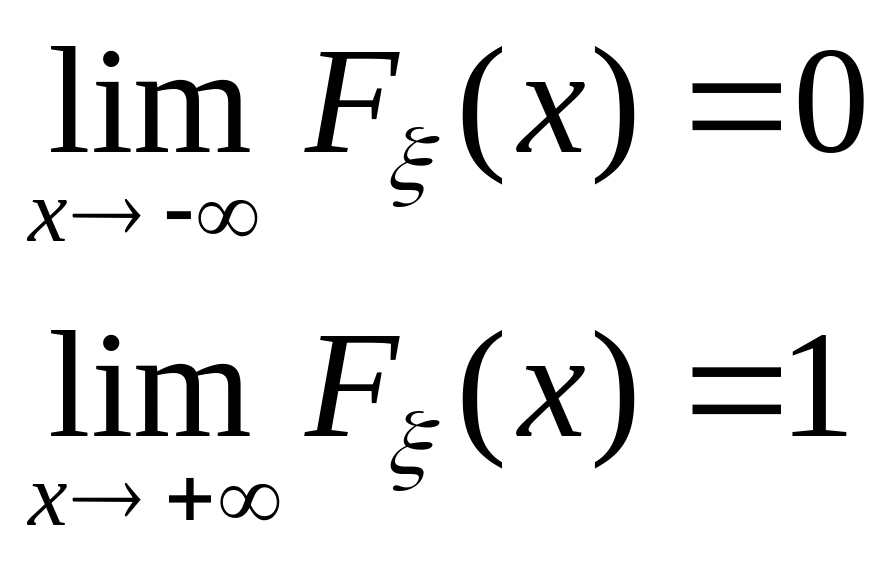
Доказательство:

Функция распределения F_ξ(x) монотонна и ограничена, следовательно, она имеет пределы:

Покажем, что а=о и b=1. Рассмотрим последовательность вложенных событий

причем пересечение множеств А_n=

Если бы пересечение было не пустым множеством, то случайная величина ξ могла бы принимать значения, меньшие любого отрицательного числа, однако таких значений не существует. В случае, если пространство элементарных событий дискретно, вероятность обладает свойством непрерывности, следовательно,

откуда вытекает

Рассмотрим последовательность несовместных событий

Тогда событие

является достоверным событием, и, согласно аксиоме счетной аддитивности

5) Функция распределения непрерывна слева, т.е.

6) P(ξ≥x)=1- F_ξ(x). Т.к. событие ξ≥x является противоположным событию ξ<x.

Таким образом, функция распределения является неубывающей, непрерывной слева и ограниченной слева функцией, которая удовлетворяет предельным равенствам F_ξ(-∞)=0 и F_ξ(+∞)=1. Любая функция, удовлетворяющая этим свойствам, может быть функцией распределения какой-то случайной величины.

20. Случайная величина ξ(ω), заданная в вероятностном пространстве {Ω, ,P}, называется непрерывной (абсолютно непрерывной), если существует неотрицательная функция f_ξ(х) такая, что при любых х функцию распределения F_ξ(x) можно представить в виде интеграла

Функция f_ξ(х) называется функцией плотности распределения вероятностей.

Свойства функции плотности распределения fξ(X):

1. f_ξ(x)≥0 т.к. в точках непрерывности плотность распределения вероятностей равна производной ф-ции распределения и (F_ξ(x))’=f(x)≥0;

2.

3. В точках непрерывности плотность распределения равна производной функции распределения: f_ξ(x)= F’_ξ(x);

4. Плотность распределения определяет закон распределения случайной величины, так как определяет вероятность попадания случайной величины на интервал [a;b):

5. Вероятность того, что непрерывная случайная величина ξ примет значение а, равна 0: P(ξ=а)=0.

Представим событие А={ω: (ξ=a)} в виде произведения

и воспользуемся аксиомой непрерывности.

Поэтому справедливы следующие равенства:

График функции плотности распределения называется кривой распределения.

Площадь, ограниченная кривой распределения и осью абсцисс, равна 1.

Непрерывная случайная величина ξ имеет равномерное распределение на отрезке [a;b], если ее плотность распределения f_ξ(х) сохраняет постоянное значение на этом промежутке:

х_med=Mξ

х_mod - любое число из отрезка [a;b]

β_ξ=0 - коэффициент асимметрии

γ_ξ=-6/5 коэффициент эксцесса

Непрерывная случайная величина ξ, принимающая неотрицательные значения, имеет показательное распределение с параметром λ>0, если плотность распределения вероятностей случайной величины равна

х_med=ln(2)/λ

х_mod=0

β_ξ=2 - коэффициент асимметрии

γ_ξ=6 коэффициент эксцесса

21. Пусть в дискретном вероятностном пространстве (Ω, , Р) задано несколько случайных величин ξ₁(ω), ξ₂(ω), …, ξ_n(ω). где ω Ω. Такой упорядоченный набор случайных величин называется случайным вектором или n-мерной случайной величиной и обозначается ξ(ω)={ξ₁, ξ₂,…, ξ_n}.

Совокупность вероятностей р_ij для любых i и j называется совместным законом распределения двумерной случайной величины (ξ₁,ξ₂), или распределением случайной величины (ξ₁,ξ₂).

Рядом распределения дискретной случайной величины ξ называется таблица, в которой перечислены все возможные значения этой случайной величины и соответствующие им вероятности.

Набор p_ij…k называется совместным законом распределения вероятностей n-мерной случайной величины (ξ₁,ξ₂,…,ξ_n) или распределения случайного вектора ξ=(ξ₁,ξ₂,…,ξ_n).

Зная совместный закон распределения, можно найти законы распределения составляющих.

{ω: ξ₁=x_i}={ω: ξ₁=x_i, ξ₂=y_j} {ωi: ξ₁=x₁, ξ₂=y₁} …. {ω: ξ₁=x_i, ξ_m=y_m}.

С ледовательно,

Условие независимости 2-мерной случайной величины:

P(ξη)= P(ξ)P(η).

22. Функция F(x₁,x₂…x_n) n аргументов называется n-мерной функцией распределения случайного вектора ξ=(ξ₁,ξ₂,…,ξ_n), или совместной функцией распределения вероятностей случайных величин ξ₁,ξ₂,…,ξ_n.

Это общее определение верно как в непрерывном, так и в дискретном случаях.

Многомерная функция распределения обладает теми же свойствами.

1. 0≤F(x₁…x_n)≤1

2. F(x₁…x_n) является неубывающей функцией по каждому из аргументов.

3. Многомерная функция распределения непрерывна по каждому из аргументов.

4. Справедливы следующие предельные ограничения:

F(+∞,+∞,…,+∞)=1,

5. Функция распределения должна быть такой, что вероятность попадания случайного вектора в n-мерный треугольник должна быть выражена через вер. и быть неотрицательной.

P(a₁< ξ₁<b₁,…,a_n< ξ_n<b_n)=F(b1,…bn)-

23. Случайные величины ξ₁,ξ₂,…,ξ_n в дискретном вероятностном пространстве (Ω, ,P) называются независимыми, если

P(ξ₁=x_i,ξ₂=y_j,…,ξ_n=z_k)=P(ξ₁=x_i)P(ξ₁=x_i)…P(ξ_n=z_k)

для любых наборов фиксированных значений (x_i,y_j,…,z_k).

Для пары (ξ₁;ξ₂) независимость означает, что для любых наборов индексов i и j, вероятность совместного появления событий (ξ₁=х_i) и (ξ₂=y_j) равна произведению вероятностей этих событий P(ξ₁=х_i;ξ₂=y_j)=P(ξ₁=х_i)P(ξ₂=y_j).

Теорема

Если случайные величины ξ₁ и ξ₂ независимы, то события В1 и В2, которые индуцируются этими случайными величинами, независимы.

Доказательство:

т.е. нужно доказать, что

Следствие: если случайные величины независимы, то F(x₁…x_n)=F₁(x₁)…F_n(x_n)

35.Нормальное распределение.

Неприрывная случайная величина называется распределенной по нормальному закону с параметрами a и σ² , если ее плотность распределения равна

Через N(a;σ²) обозначается множество всех случайных величин, распределенных по нормальному закону с параметрами a и σ².

График плотности вероятностей нормального распределения называется кривой Гаусса.

Функция распределения нормально распределенной случайной величины равна

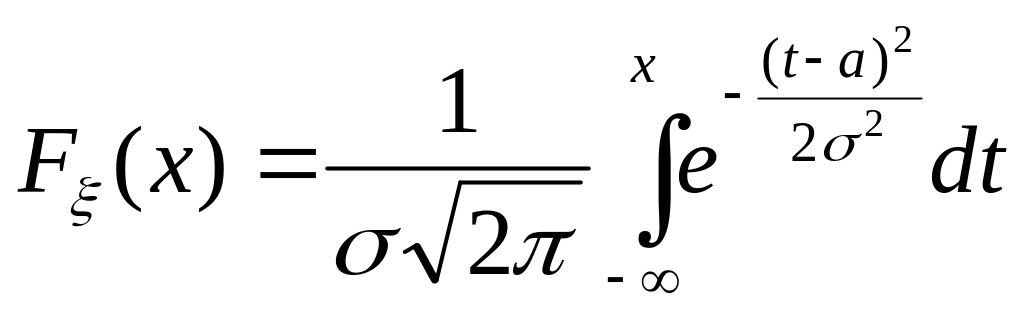
Правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

36. Стандартной нормальной случайной величиной называется случайная величина с параметрами а=0 и σ²=1. Обозначается ξ N(0;1).

Плотность распределения равна

Функция φ_ξ(х) четная и табулированная.

Функция распределения стандартной случайной величины имеет вид:

μ_k=(k-1) σ² μ_k-1

Mξ= σ² (?)

β_ξ=0 - коэффициент асимметрии

γ_ξ=0 - коэффициент эксцесса

Правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.