1. Основные понятия теории вероятностей. Частотная интерпретация вероятности. Свойство статистической устойчивости частот.

2. Дискретное пространство элементарных событий. Случайные события. Операции над событиями и их свойства.

3. Определение вероятности в случае дискретного пространства. Теоремы сложения.

4. Классическая вероятностная модель и условия ее применимости.

5. Элементы комбинаторики: выбор с возвращением, без возвращения, одновременный выбор, перестановки.

6. Статистики Бозе-Эйнштейна, Ферми-Дирака, Максвелла-Больцано.

7. Понятие теории меры и их использование в построении вероятностного пространства общего вида. Примеры, приводящие к построению общей (не дискретной) вероятностной модели. Сигма-алгебра событий. Примеры сигма- алгебр.

8. Теория А.Н. Колмогорова при построении общей вероятностной модели. Аксиоматическое построение вероятностей (вероятностной меры). Аксиомы счетной аддитивности и непрерывности. Доказать теорему об их эквивалентности.

9. Вероятность в дискретном пространстве элементарных исходов как частный случай вероятностной меры. Построение вероятностных мер на прямой и плоскости. Геометрическая вероятность.

10. Условная частота, условная вероятность и их свойства. Теорема умножения вероятностей (доказательство).

11. Полная группа событий. Формула полный вероятностей (вывод). Формула Байеса (вывод).

12. Независимые события. Независимость попарная и в совокупности. Пример Бернштейна.

13. Независимые испытания Бернулли (построения пространства и задания вероятностей элементарных исходов). Доказать теорему о распределении числа успехов в независимых испытаниях Бернулли.

14. Наивероятнейшее число успехов в n независимых испытаниях Бернулли.

15. Формула Пуассона (вывод). Условия применимости приближенной формулы Пуассона.

16. Приближенные вычисления вероятностей в схеме Бернулли. Формулировка теорем Муавра-Лапласа.

17. Полиномиальная схема. Понятие о цепях Маркова.

18. Определение случайной величины в дискретном вероятностном пространстве. Законы распределения дискретных случайных величин: биномиальное, пуассоновское, геометрическое и отрицательно биномиальное распределения..

19. Функция распределения случайной величины и её свойства (доказательства).

20. Непрерывные случайные величины. Функция плотности и её свойства (доказательства). Показательное и равномерное распределения.

21. Случайный вектор. Совместное распределение дискретных случайных величин Ряд распределения. Формулы для вычисления частных распределений.

22. Совместная функция распределения нескольких случайных величин, её свойства (доказательства).

23. Независимость случайных величин. Попарная независимость. Доказать теорему о том, что из независимости случайных величин xi (i=1,...,n) следует независимость событий {xiÎDi}, где Di конечные или счетные объединения промежутков (отрезков, полуотрезков, интервалов, полуинтервалов).

24. Теорема о совместной функции плотности независимых случайных величин (доказательство).

25. Формулы для вычисления вероятности попадания случайного вектора в некоторую область (дискретный и непрерывные случаи): P((x,h)ÎD).

26. Функция от случайных величин. Композиция законов распределения. Найти плотность распределения суммы двух случайных величин, равномерно распределенных на отрезках и , распределенных по показательному закону. Закон Симпсона.

27. Математическое ожидание дискретной случайной величины и её свойства (доказательства).

28. Математическое ожидание непрерывной случайной величины и её свойства (доказательства).

29. Математическое ожидание функции от случайной величины и её свойства (доказательства).

30. Дисперсия случайной величины и её свойства (доказательства).

31. Примеры вычисления математического ожидания и дисперсии случайных величин, распределенных геометрически, по законам Бернулли и Пуассона.

32. Ковариация, коэффициент корреляции. Доказательства их свойств.

33. Моменты высших порядков. Асимметрия, эксцесс.

34. Законы распределения непрерывных случайных величин: равномерный, показательный, Лапласа, Коши, Паретто, Вейбулла и их основные числовые характеристики.

35. Нормальное распределение. Математическое ожидание и дисперсия нормальной случайной величины. Моменты высших порядков. Асимметрия, эксцесс.

36. Стандартная случайная величина. Использование таблиц функции Лапласа при вычислении функции нормального распределения. Правило трех сигм.

37. Доказать, что любая нормальная случайная величина является линейный преобразованием стандартной нормальной величины. Теорема о распределении суммы двух независимых нормальных случайных величин.

38. Логарифмически нормальное распределение. Найти его функцию плотности.

39. Производящая функция.

40. Неравенства Маркова и Чебышева (дискретный и непрерывный случаи).

41. Закон больших чисел. Теорема Чебышева (доказательство). Теорема Бернулли, как частный случай теоремы Чебышева (доказательство). Теорема Пуассона.

42. Центральная предельная теорема. Формулировка, условия применимости. Теоремы Муавра-Лапласа.

1. Теория вероятностей - наука о закономерностях случайных событий.

Под событием в теории вероятностей понимается всякий факт, который может произойти или не произойти при осуществлении определенного комплекса условий. Каждое такое осуществление называется испытанием, опытом или экспериментом.

Все события можно разделить на 3 вида U- достоверные, V- невозможные и А,В,С… - случайные.

Достоверным называется событие, которое обязательно произойдет при испытании.

Невозможным называется событие, которое заведомо не произойдет при испытании.

Случайным называется событие, которое в результате испытания может либо произойти, либо не произойти.

Предметом теории вероятностей являются вероятностные закономерности массовых случайных событий, где под массовостью понимается многократная повторяемость.

Вероятность события - численная мера степени объективной возможности этого события.

Свойство устойчивости частот.

Пусть проведено n испытаний, в каждом из которых может появиться или не появиться событие А. Посчитаем, сколько раз в этой серии эксперимент заканчивался наступлением события А. Обозначив это число через n(A) и разделив его на общее число всех повторений эксперимента, получим величину P_n(A)=n(A)/n, называемую относительной частотой наступления события А в серии из n повторений эксперимента. P_n(A) - случайная величина и может заметно меняться от одной серии испытаний к другой. При увеличении числа испытаний, случайные обстоятельства, свойственные каждому отдельному эксперименту, в массе взаимно погашаются, и частота P_n(A) проявляет тенденцию к стабилизации, приближаясь к некоторой средней величине р. Это свойство устойчивости частот.

Этот эмпирический факт, наблюдаемый при конечном числе экспериментов, положен в основу теории вероятностей. Свойство статистической устойчивости частот в этой ситуации сформулировано в теореме Бернулли.

Теорема Бернулли:

По мере неограниченного увеличения числа однородных и независимых испытаний, относительная частота события А неограниченно приближается к некоторой постоянной величине.

Число, к которому приближается относительная частота события при неограниченно растущем числе экспериментов, называется вероятностью события А и обозначается Р(А).

2. Совокупность всех возможных исходов эксперимента, (которые можно перечислить) называется (дискретным) пространством элементарных исходов и обозначается Ω.

Ω={ω₁,ω₂,…,ω_n}

Любой элементарный исход называется элементарным событием и обозначается ω.

В случае дискретного пространства конечного или счетного событием называется любое подмножество данного пространства.

Случайным называется событие, которое в результате эксперимента может либо произойти, либо не произойти.

Операции над событиями:

1) Если при всяком эксперименте, при котором появляется А, появляется В, то А влечет за собой В.

2) Если А влечет за собой В, а В влечет за собой А, то А и В равносильны.

3) Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.

4) Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.

5) Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет.

6) не А называется дополнением к событию А, если оно появляется всякий раз, когда не появляется А.

7) Симметрической разностью событий А и В называется событие С, состоящее в появлении или А, или В, но не их одновременно.

Два события А и В называются несовместными, если наступление одного из них исключает появление другого.

События А₁,А₂,…,Аn образуют полную группу событий, если в результате эксперимента непременно произойдет хотя бы одно из них.

События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.

Событие А, состоящее из всех элементарных исходов, не входящих в А, называется противоположным событием событию А.

Очевидно, что Р(А)+Р(А)=1.

Так как А и образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А + является достоверным. Следовательно,

Р( А + ) = 1. Но, так как А и несовместны, из (2.4) следует, что Р(А + ) = р(А) + р( ). Значит, р(А) + р( ) = 1, что и т. д., откуда Р(А)=1-Р(А).

Свойства действий над событиями:

1.

2.

3.

4.

5.Св-ва коммутативности:

6.Св-ва дистрибутивности:

7. Формулы двойственности или формулы де Моргана.

Любое действие над событиями можно выразить через 1) дополнение и объединение; 2) дополнение и пересечение + формулы де Моргана.

3. Говорят, что в пространстве элементарных событий, конечном или счетном Ω={ω₁,ω₂,..,ω_n} задана вероятность, если каждому элементарному событию ω_i поставлено в соответствие неотрицательное число р_i≥0 и сумма вероятностей всех элементарных исходов равна 1, т.е. вероятность события - числовая функция, определенная на пространстве элементарных событий.

Вероятностью события А называется сумма вероятностей всех элементарных исходов, входящих в А, т.е.

Теорема сложения

1) теорема сложения вероятностей несовместных событий

Вероятность объединения двух несовместных событий равна сумме их вероятностей, т.е. если А В= , то Р(А В)=Р(А)+Р(В).

Доказательство:

Проведем его для случая конечного числа исходов. Пусть пространство элементарных событий Ω={ω₁,ω₂,…,ω_n} содержит n элементарных исходов, из них n₁ благоприятны событию А и n₂ благоприятны событию В, т.е.

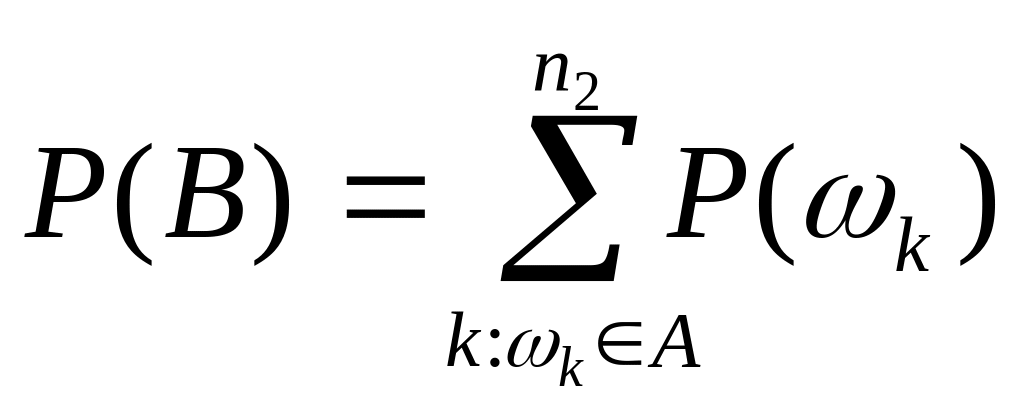
причем нет исходов, одновременно благоприятных А и В. Отсюда следует, что событию

А В благоприятны n₁+n₂ элементарных исходов и вероятность этого события вычисляется по формуле:

=P(A)+P(B) ч.т.д.

Следствия.

1. Теорему можно распространить на случай суммы любого числа слагаемых, если все события А_i попарно несовместны.

2. Р(А)+З(А)=1

3. Если А В, то Р(А)≤(В)

Теорема сложения вероятностей событий

Если события А и В пересекаются: А В=0, то

где А,В - подмножества пространства элементарных событий.

Доказательство:

Если А В - совместные события, то А В наступит тогда, когда наступит одно из несовместных событий А В, А В или А В. Согласно теореме сложения несовместных событий,

Событие А наступит, если наступит одно из несовместных событий А В, А В. Тогда вероятность события А равна

Событие В наступит, если наступит одно из несовместных событий А В или А В, и вероятность события В равна

Отсюда получаем доказательство теоремы:

Следствия

1. Вероятность пересечения 2х событий вычисляется по формуле:

2. Из т.1,2 для любых событий А и В следует Р(А В)≤Р(А)+Р(В)

3. Вероятность суммы любого числа совм. соб.:

4. Простейшей математической моделью дискретного эксперимента является т.н. классическая вероятностная модель, в которой пространство элементарных событий конечно, которое состоит из несовместных событий, организующих полную группу равновозможных событий. Такое пространство называется симметричным. Пусть Ω={ω₁,ω₂,…,ω_n} - симметричное пространство с n возможными исходами.

Р(ω_i)=p_i=p события равновероятны.

Откуда Р=1/n

А→N(A) (событию А благоприятно N исходов)

5. Основная теорема комбинаторики. Пусть имеется k групп, причем i-я группа содержит п элементов. Тогда общее число N способов, кото­рыми можно выбрать по одному элементу из каждой группы, определя­ется соотношением N= n₁n₂..n_k

1. Последовательный выбор с возвращением.

Пусть имеется некоторая конечная совокупность элементов {а_{, а₂,..а_n}, называемая генеральной совокупностью, и п — объем этой совокупности. Пусть эксперимент состоит в том, что из гене­ральной совокупности выбирают k элементов, причем выбор про­изводится последовательно и каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Пространство элементарных событий в этом эксперименте представ­ляется в виде Ω={ω_i=(a_i1,a_i2,…,a_ik)}, где а_im — элемент, выбранный на т шаге. Нас интересует число различных способов, которыми можно произвести последо­вательную выборку с возвращением k элементов из генеральной со­вокупности объема п. Поскольку каждый раз отобранный элемент возвращается в генеральную совокупность, выбор на каждом шаге производится из совокупности объема n, и можно считать, что выбор производится из k групп и все группы состоят из одинакового числа элементов n₁=п₂=...=n_k=п. Тогда, согласно основной теореме ком­бинаторики, число таких способов равно N=n^k, асам выбор называ­ется последовательным выбором с возвращением.

2. Выбор без возвращения.

Пусть эксперимент состоит в том, что из генеральной совокуп­ности выбирают k элементов, причем выбор производится последо­вательно и каждый отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Тогда первый элемент выбирается из совокупности объема n₁=n. Поскольку элемент не возвращается в генеральную совокупность, следующий элемент вы­бирается из совокупности, объем которой на один элемент меньше n₂=n-1, третий — из совокупности объема n₃=n-2 и т. д. Выбор k-го эле­мента производится из совокупности объема n_k=n-(k-1). Число способов, каким можно выбрать последовательно k элементов из ге­неральной совокупности объема п без возвращения в силу основной теоремы комбинаторики, равно N=n(n-1)(п-2)...(n-(k-1)). Это число равно числу размещений из n по k и обозначается N = A_n^k.

В общем случае размещениями из п по k называются любые упо­рядоченные совокупности, которые отличаются друг от друга или своими элементами, или их порядком. Формула для вычисления чис­ла размещений из п элементов по k имеет вид

3. Одновременный выбор.

Одновременный неупорядоченный выбор k элементов из гене­ральной совокупности объема n есть всевозможный набор k элемен­тов, отличающихся друг от друга хотя бы одним элементом. Число таких совокупностей по k элементов из n равно числу сочетаний из n по k и обозначается N=С_n^k.

Сочетаниями из n элементов по k называются любые неупорядо­ченные соединения, отличающиеся друг от друга только своими эле­ментами. Формула для вычисления числа сочетаний из п по k следующая:

4. Перестановки

Частным случаем размещений являются перестановки, когда k = n. Перестановками из n элементов называются упорядоченные со­вокупности, отличающиеся друг от друга только порядком входящих в них элементов. Формула для вычисления числа перестановок из n элементов имеет вид Pn=n!.

5. 1) Предположим, что п неразличимых частиц распределяются по т ячейкам. Различными считаются распределения частиц по ячейкам, отличающиеся только числом частиц, попавших в каждую ячейку. Такое распределение носит название статистики Бозе - Эйнштейна. Найдем общее число элементарных исходов в статистике Бозе - Эйн­штейна. Если считать «белый» элемент частицей, а «черный» — пере­городкой, то существует взаимно однозначное соответствие между способами выбора т — 1 «черного» элемента и размещениями частиц в статистике Бозе — Эйнштейна.

Для этого рассмотрим последовательность из п+т-1 элемен­тов и выберем из них т-1 «черный» элемент.

1 2 3 m-1

1 2 3 4 5 6 7 n+m-1

Так, на рисунке в первую ячейку попала одна частица, во вто­рую — три, третья оказалась пустой, ..., последняя, т-я ячейка, также

оказалась пустой. Поэтому общее число размещений равно C Найдем вероятность того, что в фиксированную ячейку попало ров­но k частиц (событие А). Заметим, что если в этой фиксированной ячейке уже находится k частиц, то остальные п-k частиц должны быть распределены по оставшимся т-1 ячейкам, а это можно сде­лать С = C способами. Следовательно, искомая веро­ятность равна

2) В статистике Ферми-Дирака п неразличимых частиц распре­деляются по т ячейкам (п≤т), однако в каждой ячейке не может находиться более одной частицы. Число различных элементарных исходов совпадает с числом способов, которыми можно выбрать п занятых ячеек из общего числа ячеек m, и так как порядок выбора

несуществен, то число способов равно N=С_n^m. Найдем вероятность того, что заняты k фиксированных ячеек. Пусть событие А заключа­ется втом, что заняты фиксированные k ячеек

(k ≤n). Тогда оставши­еся т-k ячеек должны быть заполнены п- k частицами , а это мож­но сделать С способами. Поэтому искомая вероятность равна

3) Предполагая, что п различных частиц распределяются по т ячей­кам без ограничений на число попавших в каждую ячейку частиц, получаем статистику Максвелла - Больцмана. Поскольку каждая из п частиц может попасть в любую из т ячеек, общее число элемен­тарных исходов равно N = тⁿ . Событие А заключается в том, что в первую ячейку попало n₁, частиц, во вторую — n₂, в m-ю — п_т частиц (п₁ + п₂ + ... + п_т = п). Число благоприятных для события А исходов подсчитаем следующим образом. В первую ячейку могут попасть любые n₁ частиц из имеющихся первоначально n частиц. Это можно сделать С_nⁿ¹ вторую ячейку нужно заполнить n₂ частицами из имеющихся n-n₁. Это можно сделать Сⁿ²_n-n1 различными способами. Продолжая эту процедуру получаем, что число благоприятных событию А способов равно:

Таким образом,

10. Прежде чем дать строгое определение условной вероятности, рассмотрим его с позиции частотной интерпретации. Пусть случай­ный эксперимент повторяется N раз. При этом событие А появляет­ся в этой серии N(A) раз, а событие В - N(B) раз. Обозначим через N(AB) число тех повторений эксперимента, которые закончились одновременным появлением событий А и В. Тогда N(A)/N — частота наступления события A, a N(AB)/N(B) — доля тех случаев, когда экс­перимент заканчивался наступлением события А среди только тех случаев, в которых обязательно происходило событие В. Это число называется условной частотой наступления события А при условии, что событие В произошло, или, коротко, условной частотой события А при условии события В.

В соответствии с частотной интерпретацией вероятности, сфор­мулированной в теореме Бернулли, при N→∞ частота события N(A)/N стремится к вероятности события Р(А). Покажем, что услов­ная частота также «имеет предел»:

Предел условной частоты естественно назвать условной ве­роятностью события А при условии В и обозначить Р(А/В). Тогда из полученного соотношения следует, что Р(А/В) = Р(АВ)/Р(В) как пределы одной и той же последовательности. Эти рассуждения приводят нас к математическому определению понятия «условная вероятность».

Условной вероятностью Р(А/В) события А при условии В (Р(В)>0), называется число P(А/B), равное:

Свойства условной вероятности:

1) 0≤ Р(А/В)≤1

2) Р(А/В)=1- Р(А/В)

3) Р(А/А)=1

4) Р([A₁+A₂]/В)= Р(А₁/В)+Р(А₂/В)- Р(А₁ A₂/В)

5) Если A B= , то Р(А/В)=0

6) Если событие А В С, то Р(С/AВ)=1

7) Если А В, то Р(В/А)=1

Теорема умножения вероятностей.

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое из них произошло.

Док-во:

Пусть п – число возможных исходов опыта, т_А – число исходов, благоприятных событию А, т_В – число исходов, благоприятных событию В, а т_АВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда для вычисления р(В/А) множеством возможных исходов нужно считать т_А (так как А произошло), а множеством благоприятных исходов – те, при которых произошли и А, и В ( т_АВ ). Следовательно,

откуда следует утверждение теоремы.

Следствие.

Если подобным образом вычислить вероятность события ВА, совпадающего с событием АВ, то получим, что р (ВА) = р (В) · р (А/В). Следовательно, р (А) · р (В/А) = р (В) · р (А/В).

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем Р каждого последующего вычисляется при условии, что все предыдущие имели место.

11. События А₁,А₂,…,Аn образуют полную группу событий, если в результате эксперимента непременно произойдет хотя бы одно из них.

Формула полной вероятности

Пусть событие А может произойти с одним из событий В₁,В₂,…,Вn, образующих полную группу несовместных событий.. Тогда вероятность появления события А равна сумме произведения вероятностей гипотез Р(Bi) на условную вероятность события А при каждой гипотезе Bi, т.е.

Доказательство:

Т.к. В₁,В₂,…,Вn образуют полную группу, то событие B= Bi - достоверное. A B=B

Т.к. В₁,В₂,…,Вn несовместны, то пересечения ABi для любого i тоже несовместны.

Тогда

P(AB)=P(A)+P(B)-P(A B)

Тогда

P(A)=P(AB)=P(A ( Bi))=P( ABi= H(ABi)=

= P(Bi)P(A/Bi) ч.т.д.

Формула Байеса

Если событие А может появиться с одной из гипотез В₁,В₂,…,В_n, то условная вероятность гипотезы при появлении А находится по формуле:

Доказательство:

Из т. умножения

P(BiA)=P(Bi)P(ABi)=P(A)P(BiA)

Разделим на Р(А) и получим искомое.

14. Число m*, при котором биномиальные вероятности приобретают макс. значение, является наивероятнейшим числом успехов в n испытаниях Бернулли.

Теорема.

Наивероятнейшее число успехов в n независимых испытаниях Бернулли с вероятностью успеха в одном испытании, равной р, удовлетворяет соотношению np-q≤m*≤np+p причем

1) если np-q дробное число, то существует единственное m*;

2) если np-q целое число, то существует 2 наивероятнейших числа m*;

3) если m - целое число, то np=m*

Док-во: Для доказательства существования m* сравним соседние биномиальные вероятности:

- первое нер-во.

np-q≤m(p+q)