
- •1 Определение матриц. Действие над ними.
- •2. Определители матриц и их свойства
- •3 Вычисление определителей 2-го и 3-го порядков. Вычисления высших порядков.
- •6. Векторы и действие над ними. Действие над векторами, заданными своими координатами.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •1) Сложение векторов.
- •2) Вычитание векторов.
- •3) Умножение вектора на число.
- •2. Координаты вектора
- •3. Базис системы векторов.
- •7.Уравнение прямых на плоскости и их составление.
- •8. Окружность и эллипс.
- •9. Гипербола.
- •10 Парабола.
- •11. Числовые последовательности и их пределы. Арифметические свойства пределов.
- •12. Предел функции и его свойства.
- •13. Непрерывные функции и их свойства. Точка разрыва функции и их классификация.
- •Производные и дифференциалы высших порядков
- •15. Геометрический и механический смысл первой производной.
- •17. Производные высших порядков. Механический смысл второй производной.
- •18. Исследование функций с помощью производной. Построение графиков.
- •19.Функции двух переменных. Частные производные.
- •20. Неопределенный интеграл. Его свойства и методы вычисления.
- •21. Приложение определенного интеграла в геометрии.
- •28.Комплексные числа. Их формы и действия над ними в различных формах. Переход из одной формы в другую.
13. Непрерывные функции и их свойства. Точка разрыва функции и их классификация.
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
определение

Пусть ![]() и
и ![]() .
.
Функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
если для любого
,
если для любого ![]() существует
существует ![]() такое,
что для любого
такое,
что для любого
![]()
Функция
непрерывна
на множестве ![]() ,
если она непрерывна в каждой точке
данного множества.
,
если она непрерывна в каждой точке
данного множества.
В
этом случае говорят, что функция
класса ![]() и
пишут:
и
пишут: ![]() или,
подробнее,
или,
подробнее, ![]() .
.
Комментарии
Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция непрерывна в точке
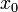 , предельной
для множества
,
если
имеет
предел в точке
,
и этот предел совпадает со значением
функции
, предельной
для множества
,
если
имеет
предел в точке
,
и этот предел совпадает со значением
функции 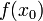 .
.Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .
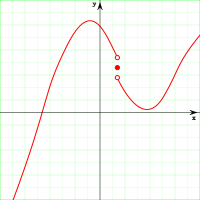
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
![]()
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если
«поправить» функцию
в
точке устранимого разрыва и положить ![]() ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением функции
до непрерывной или доопределением
функции по непрерывности, что и
обосновывает название точки, как
точки устранимого разрыва.
,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением функции
до непрерывной или доопределением
функции по непрерывности, что и
обосновывает название точки, как
точки устранимого разрыва.
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Свойства:
Локальные
Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
Если функция
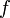 непрерывна
в точке
и
непрерывна
в точке
и 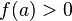 (или
(или 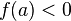 ),
то
),
то 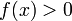 (или
(или 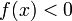 )
для всех
)
для всех 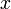 ,
достаточно близких к
,
достаточно близких к 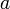 .
.Если функции и
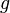 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции 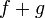 и
и 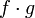 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
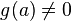 ,
то функция
,
то функция 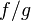 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
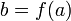 ,
то их композиция
,
то их композиция 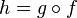 непрерывна
в точке
.
непрерывна
в точке
.
Глобальные
