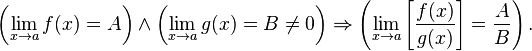11. Числовые последовательности и их пределы. Арифметические свойства пределов.
Числовая последовательность — это последовательность элементов числового пространства.
Определение:
Пусть
множество 
—
это либо множество вещественных чисел 
,
либо множество комплексных чисел 
.
Тогда последовательность 
элементов
множества
называется числовой
последовательностью.
Примеры:
Функция
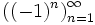является
бесконечной последовательностью целых
чисел. Начальные отрезки
этой последовательности имеют вид 
.Функция
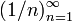является
бесконечной последовательностью рациональных
чисел. Начальные отрезки
этой последовательности имеют вид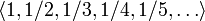 
.Функция, сопоставляющая каждому натуральному числу
одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида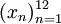 
.
В частности, пятым членом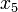 
этой
последовательности является слово
«май».
Предел последовательности
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Арифметические свойства
Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.
Однородность. Константу можно выносить из-под знака предела.
Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.
Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
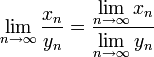
12. Предел функции и его свойства.
Определения:
Рассмотрим функцию 
,
определённую на некотором множестве
,
которое имеет предельную
точку 
(которая,
в свою очередь, не обязана ему принадлежать).
Значение 
называется пределом (предельным
значением) функции
в
точке
,
если для любой последовательности точек 
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции 
сходится
к
.[1]
Эквивалентность определений
Все данные выше определения предела функции в точке эквивалентны.[1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.
Свойства пределов числовых функций
Пусть
даны функции 
и 
.
Одна и та же функция в одной и той же точке может иметь только один предел.
Доказательство
Сходящаяся функция локально сохраняет знак. Более обще,
где 
—
проколотая окрестность точки 
.
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
Сходящаяся функция локально ограничена в окрестности предельной точки:
Отделимость от нуля функций, имеющих предел, отличный от нуля.
Операция взятия предела сохраняет нестрогие неравенства.
Правило двух милиционеров
Предел суммы равен сумме пределов:
Предел разности равен разности пределов:
Предел произведения равен произведению пределов:
Предел частного равен частному пределов.
