8. Окружность и эллипс.
Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки.
Уравнение окружности имеет вид
(x - a)2 + (y - b)2 = r2,
где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид
x2 + y2 = r2.
Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).
Простейшее уравнение эллипса
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение
a2 - b2 = c2.
Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.
Пример задач: Написать уравнение окружности с центром в точке C(2, -3) и радиусом, равным 6.
Показать, что x2 + y2 + 4x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.
Найти координаты центра и радиус окружности x2 + y2 - x + 2y - 1 = 0.
Дана окружность x2 + y2 = 4. Составить уравнение прямой l, параллельной оси абсцисс и пересекающей окружность в таких точках M и N, чтоMN = 1.
Найти длину хорды, образующейся при пересечении прямой x + y - 5 = 0 и окружности (x + 1)2 + (y + 2)2 = 40.
Найти точки пересечения окружности (x - 1)2 + (y - 2)2 = 4 и прямой y = 2x.
Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).
Найти уравнение окружности, касающейся оси Ox в начале координат и пересекающей ось Oy в точке A(0, 10).
Составить простейшее уравнение эллипса, зная, что: а) его полуоси a = 6, b = 4; б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16; в) большая полуось a = 12, а эксцентриситет e = 0,5; г) малая полуось b = 8, а эксцентриситет e = 0,6; д) сумма полуосей a + b = 12, а расстояние между фокусами 2c=6*21/2.
Найти длины осей, координаты фокусов и эксцентриситет эллипса 4x2 + 9y2 = 144.
Составить уравнение окружности, проходящей через точку A (2; 1) и касающейся осей координат.
Отрезок BC длины l движется своими концами по сторонам прямого угла BOC. Какую линию опишет на этом отрезке точка A, разделяющая его в отношении λ(BA/AC = λ)?
Составить уравнение окружности, вписанной в треугольник, стороны которого лежат на прямых x = 0, y = 0 и 3x + 4y - 12 = 0.
Составить уравнение окружности, описанной около треугольника, образованного прямой 3x - y + 6 = 0 и осями координат.
9. Гипербола.
Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
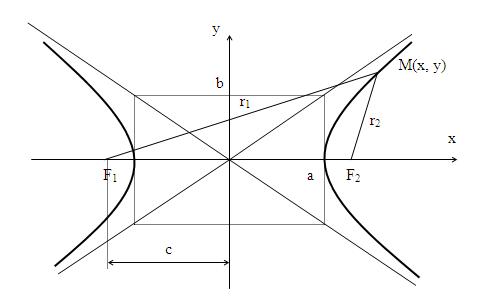
По определению | r 1 – r 2 | = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .
Выберем на гиперболе произвольную точку М(х, у). Тогда :
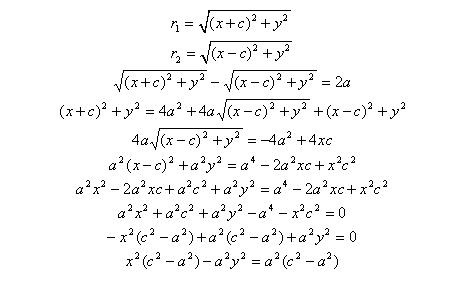
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью.
Ось 2 b называется мнимой осью.
Гипербола
имеет две асимптоты, уравнения которых 
Определение. Отношение 
называется эксцентриситетом гиперболы,
где с – половина расстояния между
фокусами, а – действительная полуось.
С учетом того, что с2 – а 2 = b2
:
Если
а = b , e = 
,
то гипербола называется равнобочной
(равносторонней).
Определение. Две
прямые, перпендикулярные действительной
оси гиперболы и расположенные симметрично
относительно центра на расстоянии a/e
от него, называются директрисами гиперболы.
Их уравнения: 
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.
Доказательство. Изобразим схематично гиперболу.
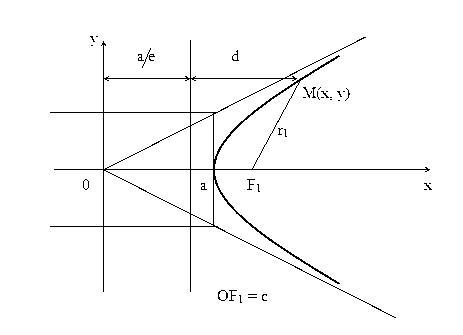
Из очевидных геометрических соотношений можно записать:
a / e + d = x , следовательно d = x – a / e .
( x – c ) 2 + y2 = r 2
Из
канонического уравнения: 
,
с учетом b2 = c2 – a2:
Тогда т.к. с/ a = e , то r = ex – a .
Итого: 
Для левой ветви доказательство аналогично. Теорема доказана
Пример
1 . Найти уравнение гиперболы, вершины
и фокусы которой находятся в соответствующих
вершинах и фокусах эллипса 
Для эллипса: c 2 = a2 – b2 . Для гиперболы: c2 = a2 + b2 .
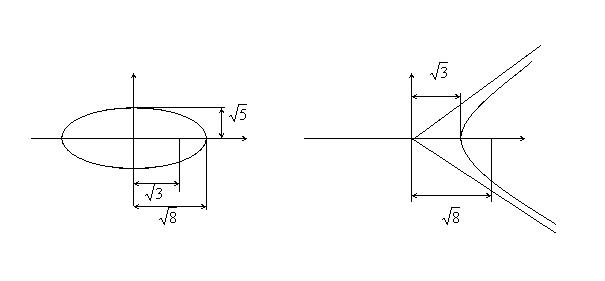
Уравнение
гиперболы:
Пример
2 . Составить уравнение гиперболы,
если ее эксцентриситет равен 2, а фокусы
совпадают с фокусами эллипса с уравнением 
Находим фокусное расстояние c 2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a2 ; a2 = 4;
b2 = 16 – 4 = 12.
Итого: 
-
искомое уравнение.