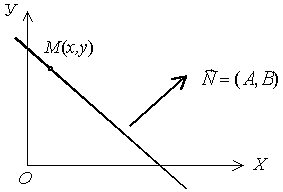3. Базис системы векторов.

 Определение. Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространству R.

Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.

Пример. 

Определение. Любой вектор вида   =  называется линейной комбинацией векторов  . Числа   -коэффициентами линейной комбинации.

Пример.  .

Определение. Если вектор    является линейной комбинацией векторов  , то говорят, что вектор   линейно выражается через векторы  .

Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.

Пример. Система векторов   линейно-зависима, т. к. вектор  .

Определение базиса. Система векторов образует базис, если:

1) она линейно-независима,

2) любой вектор пространства через нее линейно выражается.

Пример 1. Базис пространства  :  .

 2. В системе векторов    базисом являются векторы:  , т.к.  линейно выражается через векторы  .

Замечание. Чтобы найти базис данной системы векторов необходимо:

1)     записать координаты векторов в матрицу,

2)    с помощью элементарных преобразований привести матрицу к треугольному виду,

3)     ненулевые строки матрицы будут являться базисом системы,

4)    количество векторов в базисе равно рангу матрицы.

7.Уравнение прямых на плоскости и их составление.

 Всякую прямую на плоскости в прямоугольных координатах ХОУ можно описать линейным уравнением первого порядка относительно двух переменных: х и у.

О п р е д е л е н и е 1. Общим уравнением прямой на плоскости называется уравнение вида

Ax+By+C=0.                                                                  (3.1)

Рис. 39

Здесь M (x,y)   - координаты текущей точки прямой. Вектор   перпендикулярен данной прямой (рис. 39).

О п р е д е л е н и е 2. Вектор  , перпендикулярный прямой, называется нормальным вектором данной прямой. В качестве нормального вектора может быть взят любой вектор, перпендикулярный прямой.

Если на прямой задана фиксированная точка M (x₀,y₀) и нормальный вектор  , то уравнение прямой, проходящей через фиксированную точку M (x₀,y₀) перпендикулярно вектору   имеет вид

A (x-x₀) + B ( y-y₀) = 0.                                                                (3.2)

Покажем, что уравнение (3.2) является общим уравнением прямой. Для этого раскроем скобки и запишем свободный член

A x + By + (-Ax₀ - By₀) = 0.

Обозначим C = -Ax₀ - By₀, получим уравнение (3.1)

Ax + By + C=0.

Задача 1. Составить уравнение прямой, проходящей через точку M₀ = (2, -3) перпендикулярно вектору  .

Решение. Будем использовать уравнение (3.2):

.

Ответ: -3x + y + 9 = 0.

Задача 2. Составить уравнение прямой, проходящей через точку M₀ = (-1, 2) перпендикулярно оси ОХ.

Решение. Будем использовать уравнение (3.2). В качестве нормального вектора возьмем любой вектор, лежащий на оси ОХ, например,  :

.

Ответ: x + 1 = 0.

Прямая на плоскости может быть задана одним из уравнений:

1 ⁰. Общее уравнение прямой:

Ax + By + C = 0.                                                           (2.1)

Вектор n (А,В) ортогонален прямой, числа A и B одновременно не равны нулю.

2 ⁰. Уравнение прямой с угловым коэффициентом:

y - y _o = k (x - x _o ),                                                          (2.2)

где k - угловой коэффициент прямой, то есть k = tg a , где a - величина угла, образованного прямой с осью Оx, M (x _o, y _o ) - некоторая точка, принадлежащая прямой.

Уравнение (2.2) принимает вид y = kx + b, если M (0, b) есть точка пересечения прямой с осью Оy.

3 ⁰. Уравнение прямой в отрезках:

x/a + y/b = 1,                                                       (2.3)

где a и b - величины отрезков, отсекаемых прямой на осях координат.

4 ⁰. Уравнение прямой, проходящей через две данные точки -  A(x ₁, y ₁ ) и B(x ₂, y ₂ ):

.                                                       (2.4)

5 ⁰. Уравнение прямой, проходящей через данную точку A(x ₁, y ₁ ) параллельно данному вектору a (m, n):

.                                                       (2.5)

6 ⁰. Нормальное уравнение прямой:

rn ^о - р = 0,                                                             (2.6)

где r - радиус-вектор произвольной точки M(x, y) этой прямой, n ^о - единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; р - расстояние от начала координат до прямой.