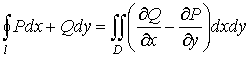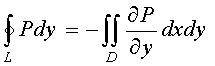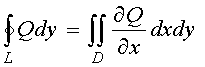20. Неопределенный интеграл. Его свойства и методы вычисления.
Неопределённый
интегра́л для функции 
—
это совокупность всех первообразных данной
функции.
Если
функция
определена
и непрерывна на промежутке 
и 
—
её первообразная, то есть 
при 
,
то
,
где С — произвольная постоянная.
Если 
,
то и 
,
где 
—
произвольная функция, имеющая непрерывную
производнуюПодведение под знак дифференциала
При подведении под знак дифференциала используются следующие свойства:
]Основные методы интегрирования
1. Метод введения нового аргумента. Если
то
где 
—
непрерывно дифференцируемая функция.
2. Метод разложения. Если
то
3. Метод
подстановки. Если 
—
непрерывна, то, полагая
где 
непрерывна
вместе со своей производной 
,
получим
4. Метод
интегрирования по частям. Если 
и 
—
некоторые дифференцируемые функции
от 
,
то
Таблица основных неопределённых интегралов
21. Приложение определенного интеграла в геометрии.
Площадь
криволинейной трапеции, ограниченной
графиком функции 
,
прямыми х = а, х = b и
осью Ох, вычисляется по формуле
(64)
Если 
,
то 
.
Пусть 
и 
–
непрерывные на 
функции
и 
при
любом 
.
Тогда площадь фигуры, ограниченной
графиками функций 
,
вычисляется по формуле
. (65)
Действительно,
если функции 
,
то данная формула является очевидным
следствием того, что площадь фигуры
равна разности площадей криволинейных
трапеций (рис. 14)
.
Если
графики функций 
и 
полностью
или частично расположены ниже оси 
,
то существует константа 
,
такая, что 
и 
.
Сделаем
замену 
(рис.
15). Тогда очевидно, что
.
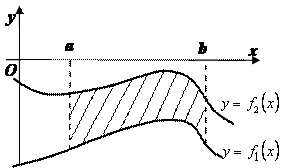
Рис. 14. Вычисление площади криволинейной фигуры |
Рис. 15. Вычисление площади криволинейной фигуры |
Пример
5.3.1. Вычислить площадь, ограниченную
графиками кривых 
и 
на
отрезке 
.
Решение. Найдем
точки пересечения графиков
и
.
Для этого решим уравнение 
.
Получаем 
и 
.
При этом 
и 
соответственно.
Таким образом, точки 
и 
–
точки пересечения данных графиков (рис.
16).
Рис. 16. Рисунок к примеру 5.3.1
Из
рисунка видно, что площадь 
,
где 
–
площадь криволинейной трапеции,
ограниченной графиком
,
а 
–
площадь криволинейной трапеции,
ограниченной графиком
.
Поэтому
.
Ответ: 
.
|
||||||
22. Двойные повторные интегралы. Сведение двойных интегралов к повторным. Определение двойного интеграла Пусть в некоторой области D на координатной плоскости XOY определена функция двух переменных z = f (x, y). Предполагается, что граница области D состоит из конечного числа кривых, заданных уравнениями вида y = f (x) или x = φ (y), где f (x) и φ (y) – непрерывные функции.
Полученная сумма называется двойной интегральной суммой. Назовем диаметром d(D) области D наибольшее расстояние между точками этой области. Обозначим через λ наибольший из диаметров частичных областей Di
О п р е д е л е н и е. Двойным интегралом называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит от способа разбиения области D, от способа выбора точек Ci,j (xi, yj) внутри каждой ячейки
В этом случае функция f (x, y) называется подынтегральной, D — областью интегрирования, x и y — переменными интегрирования, ds (или dx·dy) – элементом площади. Мы предполагаем, что функция f (x, y) ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т.е. существуют ограниченные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате { (x, y) | 0 ≤ x ≤ 1; 0 ≤ y ≤ 1} следующим образом:
Т е о р е м а 1. Функция f (x, y), непрерывная в замкнутой ограниченной области D, интегрируема в этой области. Т е о р е м а 2. Функция f (x, y),ограниченная в замкнутой ограниченной области D и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций вида y = ψ(x) или x = φ (y), интегрируема в этой области. Свойства двойных интегралов
где s — площадь фигуры D. Сведение двойного интеграла к повторному Область D называется правильной вдоль оси OY, если прямая, параллельная оси OY, пересекает границу области D в двух точках.
Пусть область правильная вдоль оси OY, нижние точки границы лежат на линии с уравнением у = φ (х), верхние — на линии с уравнением у = ψ(х). Тогда двойной интеграл можно привести к повторному
Примеры Пример
1. Вычислить
Пример
2. Вычислить интеграл
З а м е ч а н и е. Если область D не удовлетворяет условиям правильности, то необходимо область D разбить на части, каждая из которых удовлетворяла бы условиям правильности, и сводить к повторному каждый из соответствующих двойных интегралов отдельно. Формула Грина Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру L с двойным интегралом по области D, которую охватывает этот контур
Д о к а з а т е л ь с т в о: Рассмотрим правильную область по оси Oх и Oу (смотри рисунок.). Пусть область D задаётся системой неравенств: а ≤ х ≤ b, f1 (x) ≤ у ≤ f2 (x ). В совокупности линии с уравнениями у = f 1( x ) и у = f1 ( x ) образуют замкнутый контур. Рассмотрим преобразование
То есть
Аналогично доказывается
Складывая эти два соотношения, получим формулу Грина. Если в формуле Грина положить Q = x, P = − y, то получим формулу для вычисления площади плоской фигуры через криволинейный интеграл по контуру, ограничивающий область
|
||||||
|
||||||
|
||||||
|
||||||
|
.
.
.
.
.
,
,
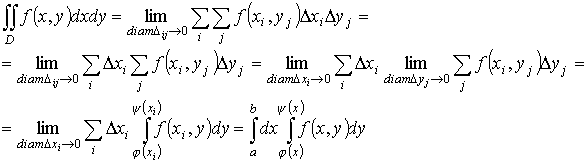
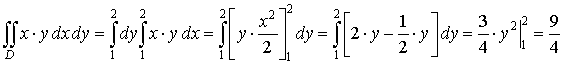где D = {(x; y)| 1 ≤ x ≤
2; 1 ≤ y ≤ 2}.
Решение.
Область интегрирования представляет
собой прямоугольник.
Преобразуя
двойной интеграл к повторному, получим
.
по области G={(x, y)|
0 ≤ x ≤ 1; 0 ≤ y ≤
1- x}.
Решение.
Область G представляет собой
треугольник, ограниченный осями
координат и прямой y = - x + 1.
Следовательно, у1(х)
= 0, у2(х) = 1 − х.
Преобразуя двойной интеграл к
повторному, получим
.
