19.Функции двух переменных. Частные производные.

Функция двух переменных

Определение. Переменная   называется функцией двух переменных   и  , если: 1) задано множество   пар численных значений   и  ; 2) задан закон, по которому каждой паре чисел   из этого множества соответствует единственное численное значение. При этом переменные   и   называются аргументами или независимыми переменными. Обозначения функций двух переменных аналогичны обозначениям функций одной переменной: ,  ,  ,   и т.д. При нахождении частного значения   функции  , которое она принимает при заданных значениях аргументов   и  , пишут   или  . Определение. Множество   всех пар значений аргументов данной функции двух переменных называется областью определения этой функции. Например, областью определения функции   является множество, для которого  . Множество   таких точек образует внутренность круга с центром в начале координат и радиусом, равным единице. Графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является в общем случае поверхность. Линией уровня функции   называется линия   на плоскости  , в точках которой функция сохраняет постоянное значение  . Аналогично   функция трех переменных.

  

 Частные производные

Пусть    -- внутренняя точка области   , и в области   задана функция   . Рассмотрим ограничение функции   на прямую   , проходящую через точку   параллельно оси   . Эта прямая задаётся условиями   при   ; переменная   может при этом произвольно меняться. Поэтому для рассматриваемого ограничения   имеется естественная параметризация, смысл которой в том, что "замораживаются" все переменные, от которых зависит   , кроме   :

Получили функцию одного переменного   , как параметризацию ограничения с помощью параметра   .

Рис.7.12.

Функция   может иметь производную в точке   , равную некоторому числу   . Это число называют частной производной функции   по переменной   , вычисленной в точке   . Эта частная производная обозначается 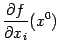  или   .

Сразу же заметим, что значения частных производных от функции   в точке   , вычисленные по разным переменным   и   , могут быть различными, так что обозначение типа   , без указания переменной, по которой вычислена частная производная, не имеет смысла: в обозначении обязательно нужно указывать переменную, по которой мы дифференцируем.

Итак, чтобы вычислить частную производную от функции   по некоторой переменной   , нужно фиксировать значения всех переменных, кроме   (то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной   . Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная.

Считая точку   , в которой вычисляется значение частной производной   , переменной точкой области   и предполагая, что во всех точках   эта производная существует, мы получаем, что частная производная 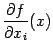   -- это функция, заданная в области   (или в её части, если производная существует не везде в   ).

Поскольку частную производную функции   можно вычислять по каждой из   переменных   , то функция   имеет   частных производных

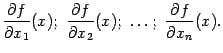
Эти частные производные, вообще говоря, -- различные функции. Их называют также частными производными первого порядка от функции   . Итак, функция   переменных имеет   частных производных первого порядка.

        Пример 7.11   Вычислим частные производные функции двух переменных

по каждой из переменных   и   .

Производную по   найдём, считая   переменной, а   постоянной величиной:

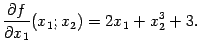
При этом мы воспользовались тем, что производная суммы равна сумме производных, тем, что производная от   (по   ) равна   , тем, что производная от   (по   , при постоянном значении   ) равна   , тем, что производная от   (по   ) равна 3, и, наконец, тем, что производная постоянного слагаемого   равняется 0.

Аналогично найдём производную по переменной   . При этом мы считаем, что    -- постоянная, а меняется только   , по которой мы и находим производную:

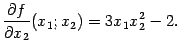
При этом слагаемые   и   постоянны, и их производная по   равна 0; в слагаемом   множитель   постоянный, и его можно вынести за знак производной, а производная от   равна   ; наконец, производная от   равняется   .     

В соответствии с изученным в первом семестре смыслом производной функции одного переменного (напомним, что производная   функции   равна скорости изменения значений функции   в точке   ), cмысл частной производной    -- это скорость изменения значений функции   при равномерном движении с единичной скоростью через точку   по прямой   , параллельной оси   .

Геометрический смысл частной производной также становится ясен, если рассмотреть ограничение   функции   , полученное при фиксации значений всех переменных, кроме   . Для наглядности ограничимся случаем функции двух переменных   и   . В этом случае мы можем изобразить график функции   на чертеже в виде некоторой поверхности.

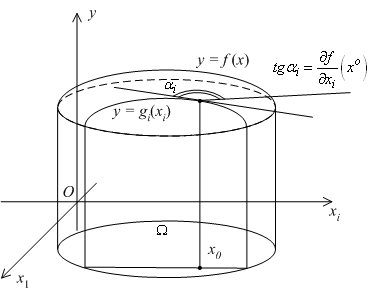
Рис.7.13.

Отметим на плоскости   точку   , в которой вычисляется частная производная 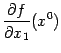  , и рассмотрим сечение графика вертикальной плоскостью   ; она проходит на плоскости   через прямую   , заданную тем же уравнением   . Тогда эта плоскость высекает в поверхности графика линию, служащую графиком функции   . Функция    -- это функция одной переменной   , и её производная в точке   равна тангенсу угла наклона касательной, проведённой к графику в точке   . С другой стороны, 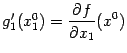  . Значит, частная производная   имеет геометрический смысл как тангенс угла наклона касательной к сечению графика   вертикальной плоскостью   .

Точно так же, частная производная   имеет геометрический смысл как тангенс угла наклона касательной к сечению графика   вертикальной плоскостью   . Заметим, что плоскости   и   взаимно перпендикулярны.

Если функция одного переменного имеет производную в некоторой точке, то эта функция обязательно непрерывна в этой точке; этот факт мы изучили в первом семестре. В случае нескольких переменных (   ) дело обстоит не так. Даже наличия в некоторой точке   частных производных функции   по всем переменным   не достаточно для того, чтобы функция была непрерывной в точке   . Приведём пример такой функции двух переменных, что частные производные её сушествуют, а функция, тем не менее, разрывна.