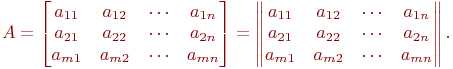1 Определение матриц. Действие над ними.

Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел a_ij, которые называют элементами матрицы и обозначается

(2.1)

Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица, которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица, это любая прямоугольная таблица, составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.

Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии

(2.1*)

Действия над матрицами и их свойства

1. Сложение матриц

Сложение: операция сложения матрицы вводится только для матриц одинаковых размеров.

Суммой двух матриц   и   называется матрица   такая, что     , например,

,   ,

тогда

.

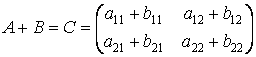Аналогично определяется разность матриц.

 

2. Умножение матрицы на число

Произведением матрицы   на число k называется матрица   такая, что     

Примечание: матрица    называется противоположной матрице  .

Операции сложения и умножения матрицы на число обладают следующими свойствами:

1)  ;

2)  ;

3)  ;

4)  ;

5)  ;

6)  ;

7)  ;

8)  .

3. Умножение матрицы на матрицу

Мы будем всегда говорить, что умножение двух матриц возможно, если число столбцов первой  матрицы равно числу строк второй матрицы:

;  ;  ;  ;   .  ,

где                                        ;      .

Например:

.

В общем случае  .

Продолжим перечисление свойств (см. п. 2.3.2):

 

9)  ;

10)  ;

11)  ;

12)  ;

13)  ;

14)  .

 

4. Элементарные преобразования матриц

К элементарным преобразованиям матриц относят:

– перестановку местами двух параллельных рядов матрицы;

– умножение всех элементов ряда матрицы на число, отличное от нуля;

– прибавление ко всем элементам  ряда матрицы соответствующих элементов параллельного  ряда, умноженных на одно и то же число. 

Две матрицы   и   называются эквивалентными, т. е.  ~ , если одна из них получается с помощью замен парных преобразований другой.

При получении элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например

.

2. Определители матриц и их свойства

Квадратную матрицу   порядка n можно сопоставить с числом   (или  , или  ), называемым определителем или детерминантом.

Вычисление определителя:

;

,

т. е. правило:

;

т. е. Правило треугольника (или Саррюса):

^.

Отметим следующие свойства определителей:

– определители не изменяются, если его строки заменить столбцами и наоборот (строки и столбцы это ряд определителя);

– при перестановке двух параллельных рядов определитель меняет знак;

– определитель, имеющий два одинаковых ряда, равен нулю;

– общий множитель элементов какого-либо рода определителя можно вынести за знак определителя;

– если элементы какого-либо ряда  определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму соответственных определителей;

– определитель не изменяется, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число;

Дальнейшие свойства связаны с понятием минора и алгебраического дополнения.

 Понятие минора

Минором некоторого элемента   определителя n -го порядка называется определитель n–1 порядка, полученный из исходного путём вычерчивания строки и столбца, на пересечении которых находится выбранный элемент.

Например, минор   элемента   матрицы третьего порядка получается вычёркиванием из матрицы второй строки и третьего столбца:

                                                                                                    

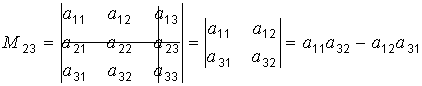
Алгебраическим дополнением элемента    определителя называется его минор, взятый со знаком «+», если сумме  – чётное число  в противном случае со знаком «–», то есть  .

Например,  ;  .

Ниже представим еще два свойства определителей:

– определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения, т. е.

 

;

 

– сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю, например:

.