9.4 Условные обозначения разных способов обсерваций

Каждое обсервованное место обозначается на карте условным знаком. Вид знака зависит от способа определения места и от типа технических средств, с помощью которых измерялись навигаци­онные параметры.

	- по визуальным пеленгам
	- с помощью РЛС
	- по спутниковым навигационным системам
	- по небесным светилам
	- методами радионавигации
	- комбинированными способами
	- обсервация, взятая под сомнение и не принятая к счислению
	- счислимообсервованное место

Контрольные вопросы:

3.1 Необходимость выполнения определения места судна.

3.2 Понятие навигационного параметра.

3.3 Понятие морского навигационного ориентира.

3.4 Понятие обсервации.

3.5 Понятие навигационной функции и навигационной изолинии.

3.6 Понятия изолиний - изоазимуты, изостадии, изогоны.

3.7 Понятия изолиний - круга равных высот, сферической гиперболы, изобаты.

3.8 Понятие линия положения.

3.9 Понятие градиента навигационного параметра.

3.10 Связь СКП навигационного параметра и СКП изолинии (линии положения).

3.11 Сущность обсервации.

3.12 Методы определения места судна.

3.13 Графические методы обсервации.

3.14 Понятие счислимо-обсервованного места.

3.15 Аналитические методы обсервации.

3.16 Графоаналитические методы обсервации.

3.17 Обобщенный метод линий положения.

3.18 Понятие невязки места судна.

9.5 Оценка точности измерений навигационных параметров

Любым измерениям, в том числе и измерениям навигационных параметров, присущи погрешности. Для оценки точности измерений необходимо произвести не одно наблюдение, а несколько – выполнить серию измерений.

Если серия измерений навигационного параметра проводилась штурманом с помощью одного и того же прибора, в небольшой интервал времени и в одинаковых условиях, то такие наблюдения можно назвать равноточными.

В качестве оценки наиболее вероятного значения для серии равноточных измерений принимают среднее арифметическое

(9.2)

где x_i – i-тое значение навигационного параметра;

n – число измерений в серии.

Когда результаты измерений выражаются многозначными числами, среднее арифметическое целесообразно вычислить по формуле

(9.3)

где x_у – удобно выбранное число.

Среднюю квадратическую погрешность (СКП) m одного измерения можно определить:

а) по формуле Бесселя для вероятных отклонений:

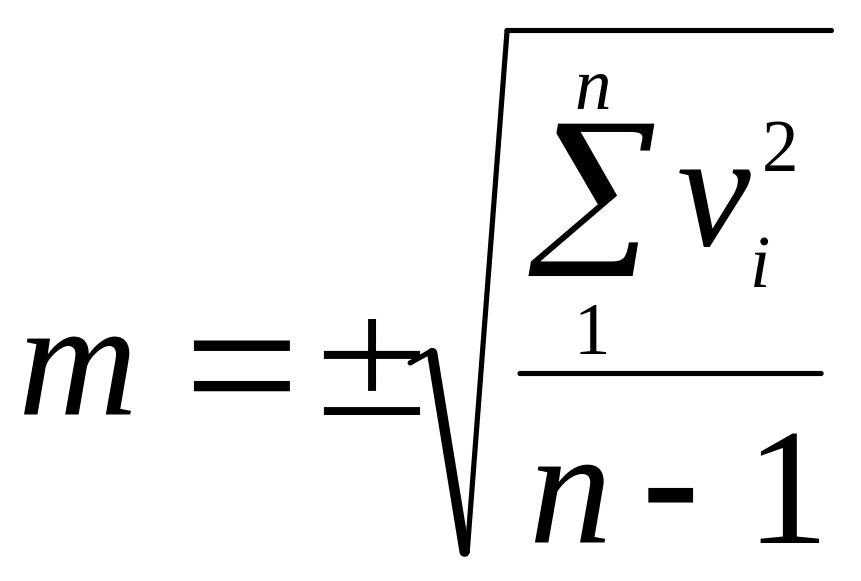(9.4)

где v_i = x_i – x₀ - вероятное отклонение.

б) по размаху

m = ± k×R (9.5)

где R – размах = x_max – x_min.

k – коэффициент, зависящий от числа измерений n.

Значение коэффициента k определяется методами математической статистики и приведено в таблице 9.1

Таблица 9.1 – Коэффициенты метода размаха

n	5	6	7	8	9	10
k	0.430	0.395	0.370	0.351	0.337	0.325

СКП наиболее вероятного значения – среднего арифметического равна

(9.6)

Предельная погрешность измерений вычисляется по формуле

Д_пр = ±3×m (9.7)

Пример. Измерена серия высот светила над видимым горизонтом. Промахи удалены, введены все соответствующие поправки, т.е. исключено влияние систематических погрешностей. Выполнить оценку точности измерений навигационного параметра.

№	ОСi	Vi = ОСi – ОС0	Vi2
1	1721,3′	-0,14	0,0196
2	17 21,8	+0,36	0,1296
3	17 21,5	+0,06	0,0036
4	17 21,3	-0,14	0,0196
5	17 21,7	+0,26	0,0676
6	17 21,5	+0,06	0,0036
7	17 21,1	-0,34	0,1156
8	17 21,3	-0,14	0,0196

Решение

Для вычисления ОС₀ по формуле (9.3) возьмем ОС_У = 17˚21,0′, тогда

ОС₀ =1721,0′ +(0,3+0,8+0,5+0,3+0,7+0,5+0,1+0,3)′ : 8 = 1721,44′.

Примечание. Промежуточные вычисления следует выполнять с точностью на порядок выше исходных данных.

а) Рассчитываем СКП одного измерения по формуле Бесселя. Для этого определим значения вероятных отклонений V_i = ОС_i – ОС₀. Затем каждое значение V_i возведем в квадрат и просуммируем

Определяем СКП одного измерения по формуле (9.4)

б) Рассчитываем СКП одного измерения по размаху.

Определяем величину размаха

R = 1721,8′ - 1721,1′ = 0,7′.

Значение коэффициента k из таблицы 9.1 для n = 8 равняется 0,351. Тогда

m = ± 0,351×0,7′ = ±0,24′.

Близость оценок СКП по формулам (9.4) и (9.5) является проверкой правильности расчетов.

П о формуле (9.6) определим СКП наиболее вероятного значения – среднего арифметического

Предельную погрешность одного измерения данной серии определим по формуле (9.7)

Д_ПР = ± 3 × 0,23 = ± 0,69′.