1. Непрерывны в замкнутом промежутке [a,b],

2. Дифференцируемы в открытом промежутке (a;b),

3. Производная g’(X)≠0 во внутренних точках интервала,

то внутри интервала существует хотя бы одна точка с, для которой имеет место равенство

Док. Т. Ферма

Предложим для определенности, что в точке с – локальный максимум.

f(c+∆x)≤f(c) ∆x<0; ∆x>0

f(c+∆x)-f(c)<0

Замечание обратное условие неверно.

Док. Т Ролля

1. f(x) – непрерывна на [a,b]=> имеет наибольшее и наименьшее м и m [a,b]-(2 теорема Вейштрасса свойство непрерывности функции)

2. М=m f(x)=const, f’(x)=0, для любых x принадлежащим [a,b]

3. M≠m, M>m существует с принадлежащее (a,b) которая по т Ферма f’(c)=0

Существует хотя бы одна точка, в которой касательная || ОХ

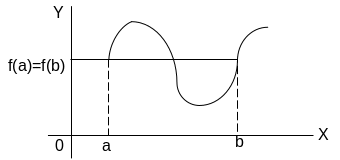
Док. Т. Лагранжа

Введем вспомогательную функцию f(x)=f(x)-f(a)-(x-a)*

Выясним геометрический смысл F(x), для этого запишем уравнение хорды АВ,

Составим уравнение хорды: y-y₀=k(x-x₀)

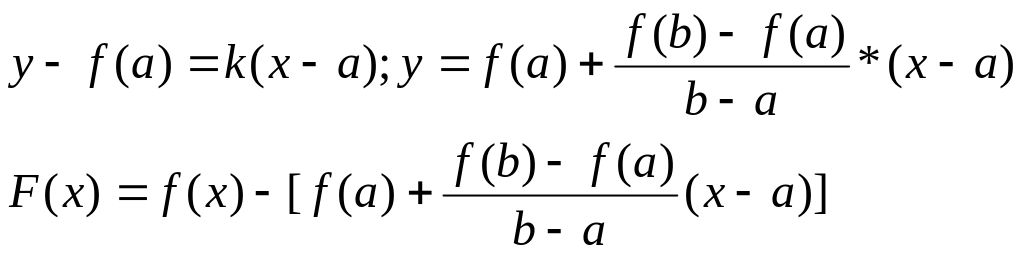
Геометрический смысл F(x): разность ординат F(a)=f(a)-f(a)-(a-a)* =0

F(b)= f(b)-f(a)-(b-a)* =0

F(a)=F(b)=0 => Для это1 функции выполняются все 3 условия теоремы Ролля согласно этой теореме существует точка с в которой F’(c)=0

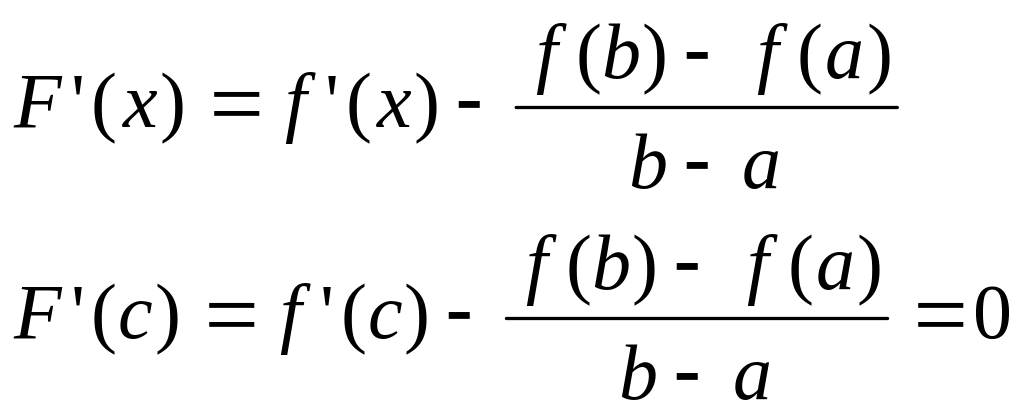
геометрический смысл этой производной: существование точки с, в которой касательная будет || хорде.

Док. Т. Коши

Составим вспомогательную функцию , где λ неопред. коэффиц Подберем λ так чтобы F(a)=F(b)

F(x)-удов услов т Ролля

1)F(x)непрерывна на [a;b] 2)F(X)дифферен на (a;b) 3)F(a)=F(b) Тогда по т Ролля на (a;b)найдется по крайней мере одна (∙)С что F `(C)=0 найдем