
- •2) → Средняя скорость не равномерное движение
- •1) Необходимость
- •Достаточность
- •1)Будем считать, что dx(первое приращение аргумента)-постоянно
- •1) Непрерывна в замкнутом промежутке [a;b],
- •2) В некоторой внутренней точке с этого промежутка достигает своего наибольшего или наименьшего значения,
- •Непрерывна в замкнутом промежутке [а; b],
- •Дифференцируема в открытом промежутке (а;b)
- •1) Непрерывна в замкнутом промежутке [a;b],
- •2) Дифференцируема в открытом промежутке (a;b),
- •Непрерывны в замкнутом промежутке [a,b],
- •Дифференцируемы в открытом промежутке (a;b),
- •Производная g’(X)≠0 во внутренних точках интервала,
Дl. Задачи, приводящие к понятию производной.
Задача 1.
S =S(t)
S
=S(t)
S
M0 M Mi
Пусть в некоторый момент времени t тело находится в точке М на расстоянии от M0, а в t + ∆T на расстоянии Mi от M0 ∆t. S(t + ∆t) – S(t) = ∆S
Рассмотрим
![]() 1)
1)
![]() →
равномерное движение
→
равномерное движение
2) → Средняя скорость не равномерное движение
∆t→0
Если существует
![]() -
скорость движение в данный момент
времени
-
скорость движение в данный момент
времени
Задача 2.
γ=γ(t) – количество вещества
t→γ(t)
t+∆t→γ(t+∆t)
∆t→γ(t→∆t)- γ(t)= ∆ γ
![]()
Д2.1. Понятие производной функции в точке.
![]() -
это предел и называется производной
функции y=f(x)
в точке х0 и обозначается
-
это предел и называется производной
функции y=f(x)
в точке х0 и обозначается
![]() (или
(или
![]() ).
).
Опр. Производной функции у=f(x) называется предел отношения функции к приращению аргумента при стремлении этого приращения к нулю.
![]() (в предложении что это предел существует)
(в предложении что это предел существует)
Если это предел существует, существует и производная в точке х0, и функция называется дифференцируемой в промежутке, если она дифференцируема в каждой точке этого промежутка.
Д2.2 Односторонние производные функции в точке.

Д3. Связь производной в точке с ее непрерывностью в этой точке.
Если функция дифференцируема в точке, то она и непрерывна в этой точке. Но из непрерывности функции в точке не следует дифференцируемость (существования производной) в точке. Поэтому при применении производной в конкретной задаче необходимо учитывать область определения как самой функции, так и ее производной.
Д4.1 Геометрический смысл производной
Из задачи о проведении касательной к графику функции =>, что угловой коэффициент касательной k=tgα=f’(x0). Поэтому с геометрической точки зрения производная f’(x0 есть tg угла наклона касательной проведенной к графику функции f(x) в (.) с абсциссой x0.
 T:
y-y0=f’(x0)(x-x0)–уравнение
касательной
T:
y-y0=f’(x0)(x-x0)–уравнение
касательной
О1)Касательной к графику функции y=f(x) в точке M0(x0,y0) называется предельное положение секущей М0М при стремлении точки М по кривой к точке М0
N:y-y0=(1/f’(x0))*(x-x0)-норм-я
прям-я(нормаль)
Значение производной функции в точке есть угловой коэффициент касательной, проведенной к графику функции данной точке.
Дифференцируемость функции в точке
с геометрической точки зрения означает,
что к графику функции в данной точке
можно провести единственную невертикальную
касательную. Если функция не дифференцируема
в точке, то это означает, что касательная
к графику функции в точке проходит
вертикально (![]() ),
или в точке к графику функции можно
провести больше, чем одну касательную
(производная не существует).
),
или в точке к графику функции можно
провести больше, чем одну касательную
(производная не существует).
Д4.2 Физический смысл производной
Значение производной функции в точке есть мгновенная скорость изменения функции в данной точке.
Физический смысл производной зависит от физического смысла рассматриваемой производной.
Положительное значение производной в точке означает, что скорость изменения функции в этой точке положительна и, следовательно, функция растет. Отрицательное же значение производной говорит о факте ее убывания.
1)S=S(t)-путь пройд-й за t при нерав-ом прям-ом движ.
∆S/∆t=Vcp на [t0,t0+∆t]; V(t0)=lim(∆t->0)∆S/∆t=S’(t0)
Мгновен-я V (.) движ. прям. и неравн. есть произ-я от пути по времени.
2)Q=Q(t) кол-во электр-а протек-го через поперечн. сеч-е пров-ка за время t.
∆Q/∆t=I
сред-я на промеж-е [t0,t0+∆t]
![]()
Сила тока в момент времени t0 есть произ-е от кол-ва эл-ва по времени
3)m=m(x) масса неоднор-й стержень в зав-ти от его длины; ∆m/∆x=ρср-сред-я плотность стержня на уч-ке[x0,x0+∆x]; ρ(x0)=lim(∆x->0)∆m/∆x=m’(x0) линейная плот-ть неод-го стержня в (.) x0 есть произ-я от массы стержня по длине.
4)m=m(t)-кол-во вещ-ва, прореаг-го за t; ∆m/∆t=Vср-средняя скор реак-и на [t0,t0+∆t]; V(t0)=lim(∆t->0)∆m/∆t=m’(t0)- скор р-и в момент t есть произ-я массы по времени
Д5.1 Правило дифференцирования. Производная суммы, разности, произведения и частного функций.
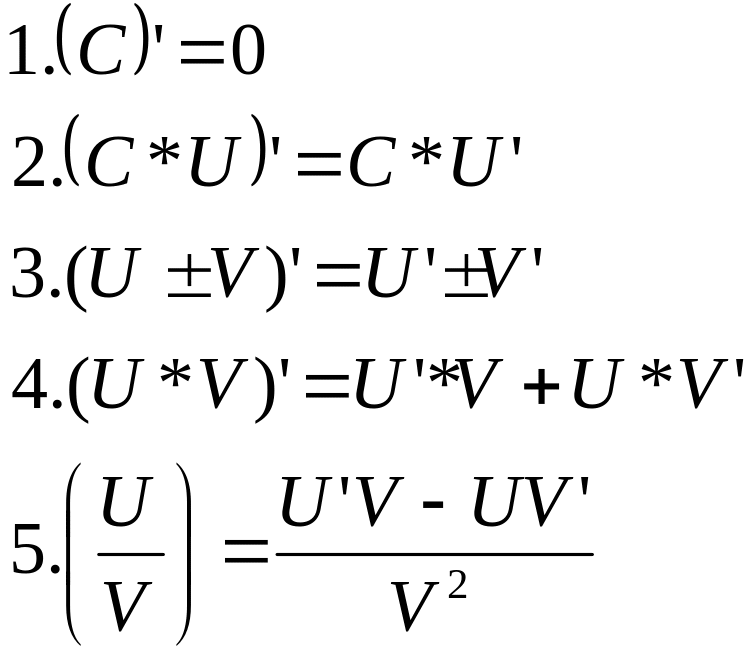

![]()
Д5.2 Производная обратной функции.
П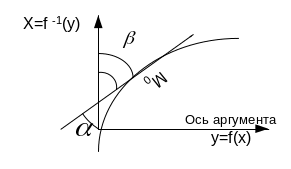 усть
у=f(x)
в точке x0.
Если существует х=f-1(y)
тогда она имеет производную в точке
y0=f(x0),
прямой
усть
у=f(x)
в точке x0.
Если существует х=f-1(y)
тогда она имеет производную в точке
y0=f(x0),
прямой
![]()
y=f(x)
x=f -1(y)

Д5.3 Производная сложной функции.
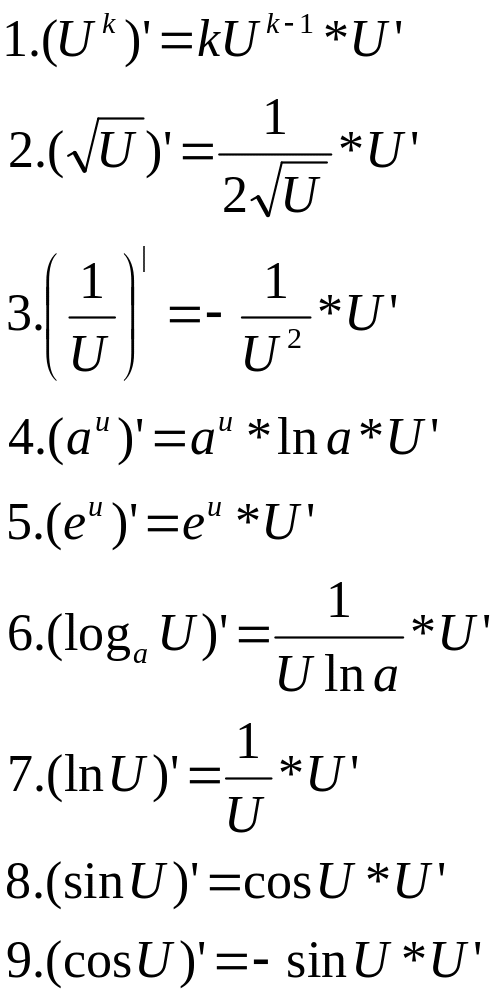
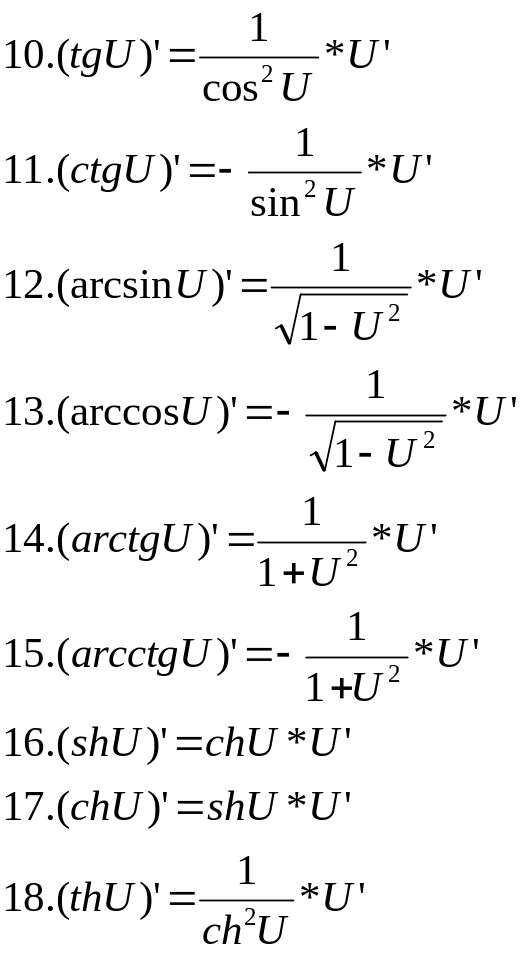
Д6.1 Понятие обратной функции, функции заданной неявно и параметрически.
Пусть функция y=f(x)
определена на X и
Y-множество ее
значений. Если каждому значению y
из Y(y![]() Y)
по тому же самому закону ставится в
соответствие единичныый элемент x
X
то говорят, что на множестве Y
определена обратная функция y=f(x).
Графики прямая и обратной функции
совпадают. Не для всякой функции можно
определять обратную функцию.
Y)
по тому же самому закону ставится в
соответствие единичныый элемент x
X
то говорят, что на множестве Y
определена обратная функция y=f(x).
Графики прямая и обратной функции
совпадают. Не для всякой функции можно
определять обратную функцию.
Т)Если функция y=f(x) строго монотонна и непрерывна на множестве X то на множестве ее значений Y существует обратная функции x=f -1(y)
y(x)=x2,
x
[0,+![]() ];
y=x2-
строго возраст и непрерывна, как
элементарная функция на [0,+
].
Следовательно на Y=[0,+
]
существует обратная функция x=y1/2.
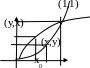
Геометрически этому преобразованию
отвечает симметричное отображение
графика f(x)
относительно биссектрисе 1 и 3-го
координатных углов.
];
y=x2-
строго возраст и непрерывна, как
элементарная функция на [0,+
].
Следовательно на Y=[0,+
]
существует обратная функция x=y1/2.
Геометрически этому преобразованию
отвечает симметричное отображение
графика f(x)
относительно биссектрисе 1 и 3-го
координатных углов.
Зам-е)Условия строгой монотонности и непрерывности функции y=f(x) является существенными для существования обратной функции.
Опр. Функция y=f(x) называется неявной функцией независимой переменной х, если она задана уравнением F(x;y)=0, не разрешаемой относительно y.
При подстановке y=f(x) в равенство F(x;y)=0 вместо у оно обращается в тождество, т.е. F(x;f(x))≡0.
Параметрически заданная функция.
Пусть на интервале (α,β) заданы 2 функции x=x(t) и y=y(t). И пусть x=x(t) строго монотонна и непрерывна на (α,β). Тогда на множестве ее значений существует обрат функция t=t(x).Подставим ее в y=y(t), получим y=y[t(x)]
Функция y=y[t(x)] заданная с помощью уравнений y=y(t) и x=x(t) t (α,β) называется заданной параметрически.
Д6.2 Дифференцирование неявно заданной функции; функции, заданной параметрически.
F(x,y) y|x -?
Если зависимость между аргументом x и функцией этого аргумента у задана уравнением, неразрешенном относительно у, то для отыскания производной от y по x надо продифференцировать этого уравнения по х, рассматривая при этом у как функцию от х. разрешая полученное уравнение (х, у, х’, y’) относительноy’. Найдем у’ по х.
Параметрически.
Пусть зависимость между аргументом х и функцией задана параметрически
![]() - параметр
- параметр
Д6.3 Логарифмическое дифференцирование
Если y=y(x)>0
![]() x
X
и функция y(x)
упрощается после логарифмирования то
целесообразно сначала найти lny(x),
а затем используя правило дифференцирования
неявно заданной функции найти y’(x)
x
X
и функция y(x)
упрощается после логарифмирования то
целесообразно сначала найти lny(x),
а затем используя правило дифференцирования
неявно заданной функции найти y’(x)
y=U(x)V(x), U(x)>0 (показательно степенная)
(lny)’x=(V(x)lnU)’x (неявно заданная функция)
(1/y(x))*y’(x)=V’(x)lnU(x)+V(x)*(1/U(x))*U’(x)
y’(x)=U(x)V(x)*[V’(x)lnU(x)+V(x)*U’(x)/U(x)]
Т.4. (О дифференциальности обратной функции)
Пусть y=f(x); x=φ(y); y’x, y’x -?
![]()
Д7. Понятие дифференцируемой функции в точке.
Определение. Дифференциалом функции у = f(х) в точке х0 называется главная линейная относительно приращения аргумента ∆х часть приращения функции ∆у. Дифференциал обозначается символом dy.
Приращение функции и ее дифференциал являются эквивалентными бесконечно малыми величинами, их разность есть величина бесконечно малая более высокого порядка малости по сравнению с каждой из них ∆y ~ dy.
Д8. Необходимое и достаточное условие существования производной в точке.
Для того чтобы функция y=f(x) имела конечную производную в точке необходимо и достаточно чтобы в некоторой окрестности этой точке ее приращения было представлено в виде

Док-во:
