7. Реляционная модель данных.Операции реляционной алгебры

Реляционная модель данных (РМД) — логическая модель данных, прикладная теория построения баз данных, которая является приложением к задачам обработки данных таких разделов математики как теории множеств и логика первого порядка.

На реляционной модели данных строятся реляционные базы данных.

Реляционная модель данных включает следующие компоненты:

• Структурный аспект (составляющая) — данные в базе данных представляют собой набор отношений.

• Аспект (составляющая) целостности — отношения (таблицы) отвечают определенным условиям целостности. РМД поддерживает декларативные ограничения целостности уровня домена (типа данных), уровня отношения и уровня базы данных.

• Аспект (составляющая) обработки (манипулирования) — РМД поддерживает операторы манипулирования отношениями (реляционная алгебра, реляционное исчисление).

Кроме того, в состав реляционной модели данных включают теорию нормализации.

Термин «реляционный» означает, что теория основана на математическом понятии отношение (relation). В качестве неформального синонима термину «отношение» часто встречается слово таблица. Необходимо помнить, что «таблица» есть понятие нестрогое и неформальное и часто означает не «отношение» как абстрактное понятие, авизуальное представление отношения на бумаге или экране. Некорректное и нестрогое использование термина «таблица» вместо термина «отношение» нередко приводит к недопониманию. Наиболее частая ошибка состоит в рассуждениях о том, что РМД имеет дело с «плоскими», или «двумерными» таблицами, тогда как таковыми могут быть только визуальные представления таблиц. Отношения же являются абстракциями, и не могут быть ни «плоскими», ни «неплоскими».

Для лучшего понимания РМД следует отметить три важных обстоятельства:

• модель является логической, то есть отношения являются логическими (абстрактными), а не физическими (хранимыми) структурами;

• для реляционных баз данных верен информационный принцип: всё информационное наполнение базы данных представлено одним и только одним способом, а именно — явным заданием значений атрибутов в кортежах отношений; в частности, нет никаких указателей (адресов), связывающих одно значение с другим;

• наличие реляционной алгебры позволяет реализовать декларативное программирование и декларативное описание ограничений целостности, в дополнение к навигационному (процедурному) программированию и процедурной проверке условий.

Операции реляционной алгебры: Выборка

Операция выборки — унарный оператор, записываемый как σ_aθb(R) или σ_aθv(R), где:

• a, b — имена атрибутов

• θ — оператор сравнения из множества {<; ≤; =; ≥; >}

• v — константа

• R — отношение (в оригинале — relation, однако как видно из примера, подразумевается не столько взаимосвязь таблиц, сколько взаимосвязь/соотношение различных фактов в рядах этих таблиц).

Выборка σ_aθb(R) (или σ_aθv(R)) выбирает все наборы значений R, для которых функция a θ b (или a θ v) будет истинна.

Проекция

Операция выборки — унарный оператор, записываемый как π_a1,…,an(R) где a₁,…,a_n — спиоск полей, подлежащих выборке. Результатом такой выборки будет набор последовательностей значений отношения R, в котором будут присутствовать только поля, перечисленные в списке a₁,…,a_n с естественным уничтожением потенциально возникающих кортежей-дубликатов[4].

Объединение

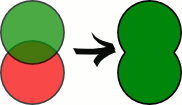
Результатом объединения отношений A и B будет отношение с тем же заголовком, что и у совместимых по типу отношений A и B, и телом, состоящим из кортежей, принадлежащих или A, или B, или обоим отношениям.

Пересечение

Результатом пересечения отношений A и B будет отношение с тем же заголовком, что и у отношений A и B, и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям A и B.

Разность

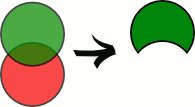
Результатом разности отношений A и B будет отношение с тем же заголовком, что и у совместимых по типу отношений A и B, и телом, состоящим из кортежей, принадлежащих отношению A и не принадлежащих отношению B.

Произведение

При выполнении прямого произведения двух отношений производится отношение, кортежи которого являются конкатенацией (сцеплением) кортежей первого и второго операндов.

Деление

Реляционное деление достаточно нетривиально описать, но на примере его смысл нагляден. В целом, из таблицы A берутся значения строк, для которых присутствуют все комбинации значений из таблицы

Соединение

Операция соединения есть результат последовательного применения операций декартового произведения и выборки. Если в отношениях и имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать.[4]