У чому полягає суть теорії квантування силових характеристик наноконтактів в моделі Зоммерфельда? Відкриті і закриті підзони.

Розглядається паралелепiпед об’ємом V=a×a×L, де L – його довжина вздовж осi z. Нерiвностi a » L i a « L вiдповiдають геометрiї вiдповiдно пластинки i нитки. Опишемо цi двi асимптотичнi межi, що iмiтують початкову i фiнальну фази видовження контакту. Це дасть змогу простежити еволюцiю енергетичних i силових характеристик 2D i 1D металевих структур.

Потенцiальне поле усерединi кластера представимо у виглядi прямокутної потенцiальної ями, глибина якої U₀< 0 i ширина L (пластинка) чи a (нитка).

Дозволенi рiвнi 2D i 1D систем, вiдрахованi вiд дна, утворюють квазiконтинуум: E_p= E_j+ E_s+ E_i. Компоненти хвильових векторiв визначають розв’язуванням рiвнянь

Густина станiв електронiв D(E) визначається сумою 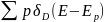за всiма заповненими станами. Замiнивши тривимiрне пiдсумовування в k – просторi iнтегруванням за k_j i k_s (чи k_i ) i пiдсумовуванням за i (або за j i s), отримаємо для нитки (чи плiвки) аналiтичний вираз для густини станiв. Наприклад, для нитки: 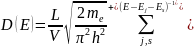(1)

Тут знак (+) у верхнiй межi пiдсумовування означає, що номери “пiдзон” j i s пробiгають значення вiд 1 до таких значень, при яких величина пiд коренем залишається додатною. Вiдповiдно кiлькiсть електронiв, наприклад, у нитцi

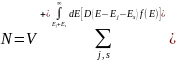
Тут функцiю розподiлу електронiв f(E) замiнимо сходинковою функцiєю θ(E – ε_F). Тодi для пластинки 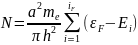(2)

де i_F – номер найвищої пiдзони, 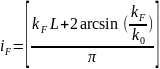(3)

[...] – цiла частина числа. Для нитки ()

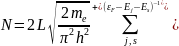Повна кiнетична енергiя всiх електронiв у нитцi

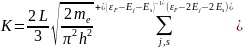(5)

Вимiрюваною характеристикою iзольованого скiнченного зразка є потенцiал iонiзацiї 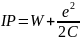(6) де C – його електрична ємнiсть. Для довгих плiвок чи ниток C → ∞, i робота виходу збiгається з потенцiалом iонiзацiї. А якщо нi, то W є тiльки корисною методично, але не вимiрюваною безпосередньо величиною. Вираз (6) можна iнтерпретувати як вплив зарядження на роботу виходу нейтрального скiнченного зразка. Розмiрна поправка W (L) конкурує з членом e²/(2C) (вони рiзного знака). Оскiльки для паралелепiпеда неможливо записати ємнiсть в аналiтичних функцiях, для оцiнки IP пластинки i нитки можна скористатися добре вiдомими виразами для ємностi сфероїдiв: диска затовшк L i голки завдовжк L.

Пружна сила має визначатися як F_Z = −dE_t/d, де E_t – сумарна енергiя електронiв та iонiв зразка. З вiрiальної теореми для кулонiвської системи в адiабатичному наближеннi випливає, що E_t = − K, тобто повна енергiя зв’язаної електронно–йонної системи негативна за знаком. Використання вiрiальної теореми є виходом за рамки одночастинкового пiдходу, у якому пiдрахувати повну потенцiальну енергiю неможливо. Пружна сила

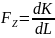
Унаслiдок використання вiрiальної теореми вираз (7) вiдрiзняється знаком вiд вiдповiдних формул у попередньому пiдроздiлi. Пiсля введення зразка в контакт з берегами хiмiчнi потенцiали електронiв вирiвнюються, й електронну систему можна розглядати як вiдкриту за умови W (L_z) = W₀ . Електронейтральнiсть кластера – пластинки чи нитки порушується, i частина електронної рiдини δN вихлюпується в резервуари, внаслiдок чого виникає контактна рiзниця потенцiалiв δφ (рис. 7.12).