
- •Викласти принципіальні результати експериментів по дослідженню стану плівок за допомогою скануючого тунельного мікроскопу
- •У чому полягає зміст магічн.Висот острівців (аналог магічн.Кластерів)
- •У яких випадках в енергетичн спектрі електронів виникають підзони?
- •У чому полягає суть теорії квантування силових характеристик наноконтактів в моделі Зоммерфельда? Відкриті і закриті підзони.
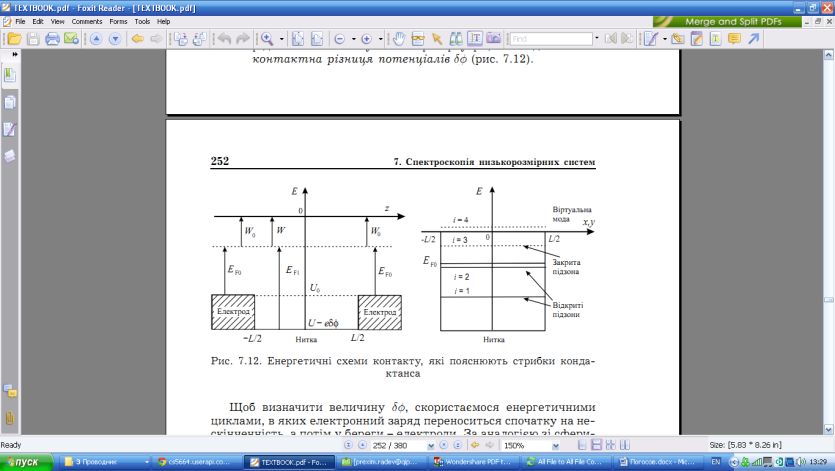
- •Р ис. 7.12. Енергетичнi схеми контакту, якi пояснюють стрибки кондактанса
- •1. Викласти принципіальні результати експериментів по дослідженню стану плівок за допомогою скануючого тунельного мікроскопу
- •У чому полягає зміст магічн.Висот острівців (аналог магічн.Кластерів
У яких випадках в енергетичн спектрі електронів виникають підзони?
Рис. 7.10. Залежнiсть кондактанса G (а) i деформацiйної сили F (б), що виникають у процесi поступового розривання “точкового” контакту мiж золотими електродами. Лiвий край горизонтальної осi вiдповiдає розриву контакту [43]: 1 – золотiй зразок; 2 – пiдтримувач зразка; 3 – кантiлiвер АСМ; 4 – золота голка
Рис. 7.12. Енергетичнi схеми контакту, якi пояснюють стрибки кондактанса
Описати експериментальні дослідження наноконтактів за допомогою атомного силового мікроскопу. У чому полягають відхилення від законів Гука та Ома в наноконтакт? Дати відповідні експериментал залежності.
Дослiдимо тонку металеву плiвку, товщина якої Lz близька до фермiївської довжини хвилi λF0 i набагато бiльша за iншi розмiри
Рис. 7.10. Залежнiсть кондактанса G (а) i деформацiйної сили F (б), що виникають у процесi поступового розривання “точкового” контакту мiж золотими електродами. Лiвий край горизонтальної осi вiдповiдає розриву контакту [43]: 1 – золотiй зразок; 2 – пiдтримувач зразка; 3 – кантiлiвер АСМ; 4 – золота голка
LX » LZ, LY » LZ, так що дискретнiс спектра проекцiй iмпульсу електрона px i py не має наслiдкiв, якi б спостерiгались. Для типової концент електронiв у металi λF0 ≃ 0,5 нм.
Профiль потенцiальної енергiї електронiв усерединi пластини в першому наближеннi можна уявити у виглядi прямокутної потенцiальної ями зi сторонами LX, LY, LZ i постiйної глибини U0< 0. У результатi розв’язування рiвняння Шредiнгера для такого потенцiалу виходить набiр хвильових чисел електрона kj = 2πj/LX, kS = 2πS/LY, j, s = 0,±1,±2,±3, ... i ki ,
i
= 1,2,3, ..., що є коренями рiвняннz
 (1)
(1)
Де
 ; me–
маса електрона. Набiр
хвильових чисел визначає енергiю
одноелектронних станiв,
по яких розподiляються
електрони:
; me–
маса електрона. Набiр
хвильових чисел визначає енергiю
одноелектронних станiв,
по яких розподiляються
електрони:
 Вiдлiк
εp
вiд
вакуумного рiвня,
тому εp
< 0. Енергiю
Фермi
для зручностi
вiдлiчуємо
вiд
плоского дна ями U
:
Вiдлiк
εp
вiд
вакуумного рiвня,
тому εp
< 0. Енергiю
Фермi
для зручностi
вiдлiчуємо
вiд
плоского дна ями U
:
 (2)
(2)
Вираз у дужках має позитивний знак, тобто в асимптотицi завжди
εF > ε0F > 0. Розмiрну роботу виходу електронiв визначаємо тривiально:
 (3)
(3)
У цьому формулюваннi W є енергетичною дистанцiєю вiд верхнього зайнятого рiвня квазiнеперервного спектра до вакуумного рiвня електронiв. Для напiвнескiнченного металу робота W вiдрiзняється вiд W0 (W < W0).
Для того, щоб визначити силовi характеристики, необхiдно обчислити розмiрнозалежну кiнетичну енергiю електронiв:
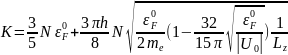 (4)
(4)
де N – кiлькiсть валентних електронiв у пластинцi. Другий доданок у дужках є поправкою на скiнченну глибину потенцiальної ями. Ця поправка дуже iстотна i становить приблизно 50 %. На вiдмiну вiд нескiнченної ями, локалiзацiя електронiв у ямi скiнченної глибини не є повною i тому кiнетична енергiя в цьому разi нижча.
