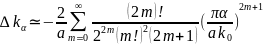У чому полягає зміст магічн.Висот острівців (аналог магічн.Кластерів)

Перспективне використання низькорозмiрних структур в нанотехнологiях стимулює численнi дослiдження їх фiзичних властивостей. Недавно вперше були проведенi вимiрення роботи виходу плiвок Ag в кiлькостi моношарiв вiд 1 до 24 на пiдшарку Fe(100).

М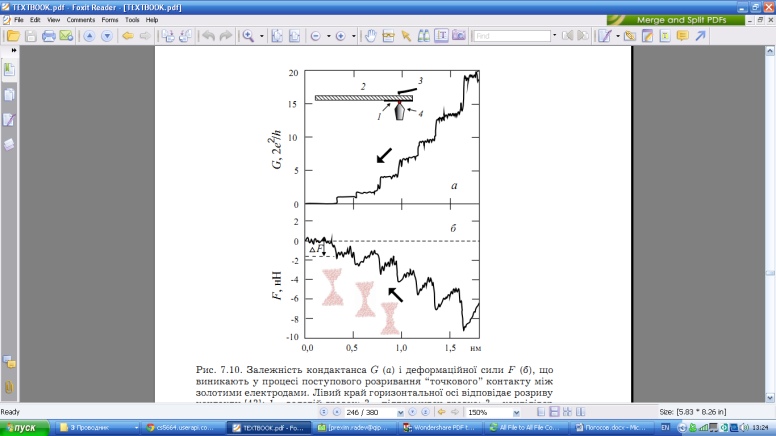 агiчнi значення товщини, яким вiдповiдають максимуми роботи виходу, дорiвнювали 3, 7, 12...15, 21...23 кiлькостям моношарiв. В iншiй роботi експериментально також виявлено магiчнi числа для висот h острiвцiв Pb на поверхнi Cu(111) [19, 20]. Дослiдження найбiльш iмовiрних висот проведено за допомогою СТМ аж до h = 23 моношару. Острiвцi мали дiаметр приблизно 50 нм, тим самим забезпечуючи одновимiрне квантування спектра в острiвцях. Магiчнi значення h = 4, 6, 8, 11, 15, 17, 20, 22 пояснюються не тiльки таким квантуванням, а й специфiчними особливостями

зонної структури Cu(111).

В експериментах, проведених на мiкрозвуженнях, сформованих у двовимiрних електронних шарах, виявлено ефект стрибкоподiбного змiнення кондактанса залежно вiд звуження, ширину якого регулювали напругою на затворi [43]. Цей ефект дослiджували в деталях, включаючи моделювання одновимiрних металевих, вуглецевих контактiв i нанотрубок.

Робота виходу електронiв плiвки вперше обчислена В.Б. Сан-домiрським. Робота виходу осцилювала поблизу свого середнього значення, яке не залежить вiд товщини плiвки. Наступнi детальнi обчислення (зокрема i ab initio) не дають однозначної iнформацiї про характер розмiрної залежностi роботи виходу iзольованих плiвок i ниток, а її осциляцiї виходять нефiзично великими.В експериментi з дослiдження точкового контакту золотих зразкiв у процесi його “видовження” аж до розриву виявилось, що осциляцiї його пружних констант виникають одночасно зi стрибкоподiбним змiненням кондактанса (рис. 7.10). “Розмiрнiсть” контакту має змiнюватися пiд час розмикання контакту. I якщо в момент утворення контакту його можна уявити як пластинку, “вставлену” в контакт, то в момент розриву контакту - це дротик або нитка. Отже, в експериментi варто говорити про перехiд вiд 2D (чи 0D) до 1D вiдкритої електронної системи.

Приблизне рішення рівняння Шредінгера для електронів провідності у плівці та острівцях (кластерах) різноманітної форми (кластери-паралелепіпеди). За яким принципом проводиться розділення змінних у рівнянні Шредінгера?

Яма-паралелепiпед. Уявiмо тривимiрну яму з вертикальними стiнками у виглядi паралелепiпеда об’ємом L_X×L_Y×L_Z. Для такої геометрiї доцiльним є використання декартової системи координат.

У цьому разi рiвняння Шредiнгера для частинки у тривимiрному потенцiалi має вигляд: 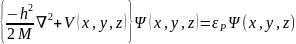(1)

Для ями з плоским дном i вертикальними стiнками потенцiал завжди можна записати у виглядi

V (x, y, z) = U₀ θ(x ± L_X /2)θ(y ± L_Y/2)θ(z ± L_Z/2) (2)

де за початок координат обрано центр ями, ступiнчаста функцiя θ(ξ ± L_ξ/2) дорiвнює 1 на промiжку –L_X,Y,Z/2 < x, y, z < +L_X,Y,Z/2 i 0 зовнi ями. Рiвняння Шредiнгера в декартових координатах дає змогу роздiлити змiннi, тому розв’язок (1) шукаємо у виглядi

Ψ(x, y, z) =Ψ (x)Ψ(y)Ψ(z) (3)

Тодi, враховуючи (1), (2),

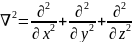
а також подаючи ε_P як суму ε_P = ε_j + ε_S+ ε_i , з рiвняння (1) отримуємо три iдентичних рiвняння для кожної iз компонент, наприклад для z компоненти

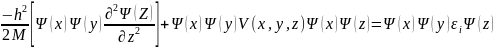
При скороченнi на 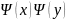рiвняння (4) набуває вигляду

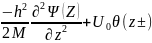де ε_i= U₀+h² k_i²/(2M), тобто енергiю вiдлiчуємо вiд рiвня енергiї частинки у вакуумi.

Аналогiчнi рiвняння можна записати i для iнших осей координат. При цьому передбачається, що часткою об’єму i поверхнi поблизу ребер i кутiв можна знехтувати. Справа в тому, що на ребрах похiднi хвильових функцiй є невизначеними i граничнi умови для зшивання функцiй неможливо виконати. Граничнi умови далеко вiд ребер i кутiв приводять до рiвняння, розв’язуючи яке, визначають компоненти хвильових векторiв. Щоб вiдрiзнити реальнi рiвнi вiд вiртуальних, у квантових точках рiзної форми необхiдно ввести критерiй

k_α /k₀ < 1, α ≡ j, s, i. (4)

Для кластера-паралелепiпеда зi сторонами L_X , L_Y , L_Z i потен-цiальним профiлем з нескiнченно високими стiнками вираз для енергетичного спектру зводиться до вигляду

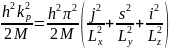
Використовуючи теорiю збурень розв’язок рiвнянь можна звести до розв’язку для нескiнченно глибокої ями. Для цього k_α подамо у виглядi

k_α = k_α^∞ + ∆k_α , ξ ≡ |∆k_α /k_α^∞| « 1, (5)

де k_α^∞= πα/L_x – розв’язок, який вiдповiдає k₀ → ∞. Пiдставляючи вираз для куба з ребром Lx = Ly = Lz ≡ a отримаємо:

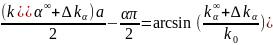
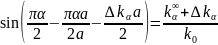
Оскiльки |∆k_α/k_α^∞| « 1, т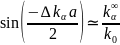о або

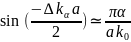
для довiльного a, але для таких α, щоб виконувалася нерiвнiсть πα/ak₀< 1. Останнiй вираз перепишемо у виглядi )

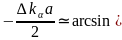Розклавши праву частину в ряд Тейлора